1 / 12

Étude comparée des dipôles RC et RL

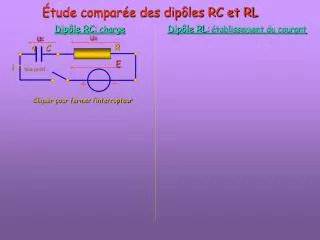
q. C. i. Étude comparée des dipôles RC et RL. Dipôle RL: établissement du courant. Dipôle RC: charge. u R. u c. R. E. Sens positif. Cliquer pour fermer l’interrupteur. u R. u c. R. q. C. E. i. E. u c. u R. 0. t. Étude comparée des dipôles RC et RL.

semah
Télécharger la présentation

Étude comparée des dipôles RC et RL

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. q C i Étude comparée des dipôles RC et RL Dipôle RL: établissement du courant Dipôle RC: charge uR uc R E Sens positif Cliquer pour fermer l’interrupteur

  2. uR uc R q C E i E uc uR 0 t Étude comparée des dipôles RC et RL Dipôle RL: établissement du courant Dipôle RC: charge Sens positif Observer les variations des tensions puis cliquer pour établir l’équation différentielle qui régit la tension aux bornes du condensateur

  3. uR uc R q C E i E uc uR Par ex à ti 0 t - t/t avec t = R.C Solution : uc = E( 1 – e ) Étude comparée des dipôles RC et RL Dipôle RL: établissement du courant Dipôle RC: charge Sens positif à tout instant : uc+ uR= E uc+ uR= E uc = q/C uR = R.i = R.dq/dt = R.C.duc/dt uc + R.C.duc/dt = E Cliquer pour continuer

  4. r,L q C R’ i i E uc uR à tout instant : uc+ uR= E Par ex à ti 0 t uc+ uR= E uc = q/C uR = R.i = R.dq/dt = R.C.duc/dt uc + R.C.duc/dt = E - t/t avec t = R.C Solution : uc = E( 1 – e ) Étude comparée des dipôles RC et RL Dipôle RL: établissement du courant Dipôle RC: charge uR uB uR’ uc R E E Sens positif Sens positif Cliquer pour fermer l’interrupteur

  5. uR uc r,L R q C R’ E E i i E- r.i E E uc uR’ r.i uR uB à tout instant : uc+ uR= E Par ex à ti 0 0 t t uc+ uR= E uc = q/C uR = R.i = R.dq/dt = R.C.duc/dt uc + R.C.duc/dt = E - t/t avec t = R.C Solution : uc = E( 1 – e ) Étude comparée des dipôles RC et RL Dipôle RL: établissement du courant Dipôle RC: charge uB uR’ Sens positif Sens positif Observer les variations des tensions puis cliquer pour établir l’équation différentielle qui régit l’intensité dans le circuit

  6. uR uc r,L R q C R’ E E i i E- r.i E E uc uR’ r.i uR uB à tout instant : uc+ uR= E Par ex à ti Par ex à ti 0 0 t t uc+ uR= E uc = q/C uR = R.i = R.dq/dt = R.C.duc/dt uc + R.C.duc/dt = E - t/t avec t = L/R - t/t Solution : i = (E/R)[1 – e ] avec t = R.C Solution : uc = E( 1 – e ) Étude comparée des dipôles RC et RL Dipôle RL: établissement du courant Dipôle RC: charge uB uR’ Sens positif Sens positif à tout instant : uB+ uR’= E uB+ uR’= E uB= r.i + L di/dt uR’= R’.i (r+R’)i + L di/dt = E R.i + L di/dt = E Cliquer pour continuer

  7. uR uc R q C E i Étude comparée des dipôles RC et RL Dipôle RL: rupture du courant Dipôle RC: décharge Sens positif Cliquer pour basculer le commutateur

  8. uR uc R q C E i E uc 0 t uR -E Étude comparée des dipôles RC et RL Dipôle RL: rupture du courant Dipôle RC: décharge Sens positif Observer les variations des tensions puis cliquer pour établir l’équation différentielle qui régit la tension aux bornes du condensateur

  9. uR uc R q C E i E uc à tout instant: uc+ uR= 0 0 t uR < 0 car avec cette convention de signe i = dq/dt < 0 uR -E - t/t avec t = R.C Solution : uc = E.e Étude comparée des dipôles RC et RL Dipôle RL: rupture du courant Dipôle RC: décharge Sens positif uc+ uR= 0 uc = q/C uR = R.i = R.dq/dt = R.C.duc/dt uc + R.C.duc/dt = 0 Cliquer pour continuer

  10. uR uB uR’ uc r,L R q C R’ E E i i Diode parfaite E uc à tout instant: uc+ uR= 0 0 t uR < 0 car avec cette convention de signe i = dq/dt < 0 uR -E uc+ uR= 0 uc = q/C uR = R.i = R.dq/dt = R.C.duc/dt uc + R.C.duc/dt = 0 - t/t avec t = R.C Solution : uc = E.e Étude comparée des dipôles RC et RL Dipôle RL: rupture du courant Dipôle RC: décharge Sens positif Sens positif Cliquer pour ouvrir l’interrupteur

  11. uR uB uR’ uc r,L R q C R’ E E i i Diode parfaite E uc à tout instant: uc+ uR= 0 0 t uR < 0 car avec cette convention de signe i = dq/dt < 0 uR -E uc+ uR= 0 uc = q/C uR = R.i = R.dq/dt = R.C.duc/dt uc + R.C.duc/dt = 0 - t/t avec t = R.C Solution : uc = E.e Étude comparée des dipôles RC et RL Dipôle RL: rupture du courant Dipôle RC: décharge Sens positif Sens positif uR’ 0 t uB Observer les variations des tensions puis cliquer pour établir l’équation différentielle qui régit l’intensité dans le circuit

  12. uR uB uR’ uc r,L R q C R’ E E i i Diode parfaite E uR’ uc R’.E R à tout instant: uc+ uR= 0 à tout instant: uB+ uR’= 0 0 0 t t uR < 0 car avec cette convention de signe i = dq/dt < 0 uB uR -E uc+ uR= 0 uc = q/C uR = R.i = R.dq/dt = R.C.duc/dt uc + R.C.duc/dt = 0 - t/t avec t = R.C - t/t Solution : uc = E.e avec t = L/R Solution : i = (E/R). e Étude comparée des dipôles RC et RL Dipôle RL: rupture du courant Dipôle RC: décharge Sens positif Sens positif uB+ uR’= 0uB= r.i + L di/dtuR’= R’.i(r+R’)i + L di/dt = 0 uB+ uR’= 0uB= r.i + L di/dtuR’= R’.i uB+ uR’= 0uB= r.i + L di/dt uB+ uR’= 0 R.i + L di/dt = 0 Cliquer pour arrêter

More Related