1 / 35

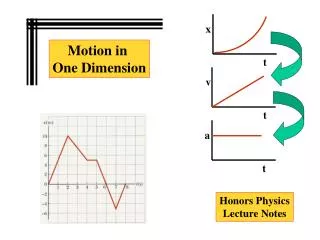
Motion in one dimension

Motion in one dimension. Test 2. Kinematics. - the branch of physics that describes motion in terms of x, v, a, and t x- position (m) (sometimes d) v- velocity (m/s) a- acceleration (m/s²) t- time (s) Dynamics is kinematics + force exerted on an object. Displacement.

sonya-holden
Télécharger la présentation

Motion in one dimension

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Motion in one dimension Test 2

  2. Kinematics • - the branch of physics that describes motion in terms of x, v, a, and t • x- position (m) (sometimes d) • v- velocity (m/s) • a- acceleration (m/s²) • t- time (s) • Dynamics is kinematics + force exerted on an object.

  3. Displacement • Defined as the change in position • f stands for final and i stands for initial • Units are meters (m) in SI • Example: If Xf = 30m and Xi = 20m what is the displacement?

  4. Distance is different than Displacement • Distance is a scalar quantity which refers to "how much ground an object has covered" during its motion. • Displacement is a vector quantity which refers to "how far out of place an object is"; it is the object's overall change in position.

  5. A physics teacher walks 4 meters East, 2 meters South, 4 meters West, and finally 2 meters North. Distance traveled would be 2m +4m + 2m +4m = 12m Displacement would be 0m, you end where you started.

  6. Displacement Xi =120m Xf = 5m ΔX= Xf - Xi ΔX= 5-120= -115 Negative displacement moves left or down; positive displacement moves right or up.

  7. Displacement Examples • From A to B • xi = 30 m • xf = 52 m • x = 22 m • The displacement is positive, indicating the motion was in the positive x direction • From C to F • xi = 38 m • xf = -53 m • x = -91 m • The displacement is negative, indicating the motion was in the negative x direction

  8. Position versus time graphs

  9. Speed • The average speed of an object is defined as the total distance traveled divided by the total time elapsed (scalar quanity) • SI units are m/s (meters per second) • Always positive

  10. Velocity • Velocity is magnitude and direction • 7 m/s East • If V is positive motion is to the right. • If V is negative motion is to the left. • Speed is the magnitude of velocity (no direction) • Velocity is a vector quanity

  11. Velocity • It takes time for an object to undergo a displacement • The average velocity is the rate at which the displacement occurs • Velocity can be positive or negative • t is always positive

  12. Speed vs. Velocity • Cars on both paths have the same average velocity since they had the same displacement in the same time interval • The car on the blue path will have a greater average speed since the distance it traveled is larger

  13. Practice problem How fast is a train moving if it travels 25 m in 5 sec? Given: Solve: X=25m V = x/t V = 25m / 5 sec t=5s V = 5 km/s

  14. Example Question • If a car travels 100 miles in 2 hours what is the velocity of the car? • ________ mph • Convert this is meters/second

  15. A car travels 40 meters between the hours of 10am and 12am. What is the cars average velocity? Example question

  16. A runner runs 3 seconds at 4m/s, stops for one second, and begins running for 2 seconds and covers 3m. • What is the velocity from (a) A to B, (b) B to C, and (c) A to D

  17. Constant Velocity • Constant velocity is when an object’s velocity remains the same for a given amount of time. • An objects current velocity would be equal to the average velocity.

  18. Acceleration • Changing velocity means an acceleration is present • Acceleration is the rate of change of the velocity • Units are m/s²

  19. Which car has the greatest acceleration? Which line goes with which car?

  20. Practice problem What is the acceleration of a car that travels from 20m/s to 50m/s in a period of 5s? Given: Solve: a = vf – vi t 20m/s = vi 50 m/s =vf a = 50m/s – 20m/s 5s 5s = t a = 6 m/s2

  21. Velocity vs acceleration

  22. We know that Vf= Vi + aΔt

  23. You need to understand that.. • Xo = Xi • X= Xf

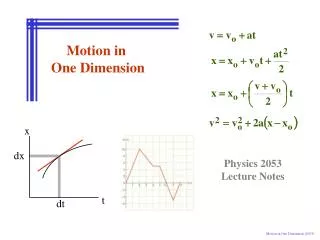
  24. Motion in One Dimension with Constant Acceleration • V= Vo + at • X – Xo= ½ (v + vo)t • X – Xo= Vo t + ½ at2 • V2 - Vo2 = 2a (X – Xo)

  25. Freely Falling Objects (3.3) An object moving under the influence of gravity alone. Regardless of its initial conditions.

  26. Freely Falling objects • Drop something • Throw something and let it fall • Throw something down • Objects thrown upward or downward and those released from rest are all falling freely once released. • Once in freefall motion all objects experience the same acceleration; downward and equal to the acceleration due to gravity. (Earths Gravity= 9.8 m/s²

  27. a= -g = 9.8 m/s² • V= Vo - gt • y – yo= ½ (v + vo)t • y – yo= Vo t - ½ gt2 • V2 - Vo2 = - 2g (y – yo)

  28. Remarks… • Air resistance is neglected. All objects regardless of there mass will move at the same rate if they have the same initial conditions • Free fall motion is symetrical

  29. JD drops a pile of roof shingles from the top of a roof located 8.52 meters above the ground. Determine the time required for the shingles to reach the ground. y-y. = v.t + 1/2gt2 -8.52m = 0 + .5(-9.8m/s2)t2 -8.52m = -4.9m/s2 t2 -8.52m/-4.9m/s2 = t2 1.7s2 =t2 1.3 s = t

  30. Practice problem Rex Things throws his mother's crystal vase vertically upwards with an initial velocity of 26.2 m/s. Determine the height to which the vase will rise above its initial height. V2 - Vo2 = - 2g (y – yo) Given: vi = 26.2 m/s vf = 0 m/s a = –9.8 m/s2 y = ?? (0 m/s)2 = (26.2 m/s)2 + 2(-9.8m/s2)y 0 m2/s2 = 686.44 m2/s2 + (-19.6 m/s2)y 0 m2/s2 -686.44 m2/s2 =(-19.6 m/s2)y -686.44 m2/s2 =(-19.6 m/s2)y y = (-686.44 m2/s2)/ (-19.6 m/s2) y = 35.0 m

  31. The observation deck of a skyscraper is 420 m above the street. Determine the time required for a penny to free-fall from the deck to the street below. y= -420m y-y.= v.t - ½ gt2 g =9.8m/s2 -420m = 0.5 (9.8m/s2)t2 -420m = -4.9m/s2t2 -420m/-4.9m/s2= t2 85.7m2/s2= t2 9.26s = t

  32. Terminal Velocity • An object that falls will experience a force due to gravity and a force due to the air. • These forces are opposite in direction. • The object will reach a point where the forces balance, which means the object will no longer accelerate. It will continue with constant velocity. • Terminal velocity is the point reached by an object where it will no longer accelerate.

  33. A Ball Thrown Up Consider a ball that is thrown straight up. • It will have maximum velocity the instant it leaves your hand and when it returns to your hand. (The ball is caught at the same height.) • On the way up, the ball will have negative acceleration, therefore the ball’s velocity will decrease.

  34. Consider a rock thrown downward from a high altitude hot-air balloon. If the initial velocity is 15 m/s and air resistance is neglected, what is the acceleration of the rock after one second? What is the velocity of the rock? 9.8 m/s2

More Related