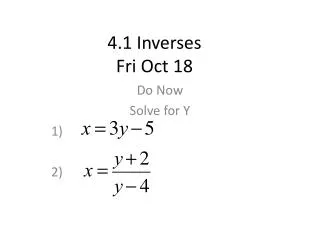1 / 7

Understanding Inverse Functions: Conditions and Properties

Inverse functions are essential in mathematics, defined by the relationship between two functions, f and g. This guide explores the conditions for f and g to be inverses of each other: g(f(x)) = x and f(g(x)) = x for all x in their respective domains. We discuss methods to determine if a function is one-to-one, which is necessary for having an inverse, including the vertical and horizontal line tests. Additionally, we examine graphical reflections about the line y = x and describe how the domain and range of functions relate to their inverses.

tariq
Télécharger la présentation

Understanding Inverse Functions: Conditions and Properties

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. If the functions f and g satisfy two conditions: Section 4.1: Inverses g(f(x)) = x for every x in the domain of f f(g(x)) = x for every x in the domain of g then f and g are inverse functions. f is an inverse of g and g is an inverse of f

  2. Determine whether f and g are inverses: Section 4.1: Inverses f and g are inverses

  3. Method for determining the inverse of a function: Section 4.1: Inverses Solve for x:

  4. A function f has an inverse if and only if its graph is cut at most once by any horizontal line: Section 4.1: Inverses A function which passes the vertical and horizontal line tests has an inverse and is one-to-one.

  5. Graphically: Section 4.1: Inverses If f has an inverse, the graphs of the functions are reflections of one another about the line y = x.

  6. If the graph of f is always increasing or decreasing, then the function f has an inverse. Section 4.1: Inverses How can we show a function is always increasing or decreasing?

  7. The domain of the original is the range of the inverse. The range of the original is the domain of the inverse. Section 4.1: Inverses

More Related