1 / 48

Transformations, Quadratics, and CBRs

Transformations, Quadratics, and CBRs. Jerald Murdock Jmurdock@traverse.com www.jmurdock.org. Based on the Discovering Algebra Texts–Key Curriculum Press. Investigation-based learning Appropriate use of technology Rich and meaningful mathematics

ulf
Télécharger la présentation

Transformations, Quadratics, and CBRs

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Transformations, Quadratics, and CBRs Jerald Murdock Jmurdock@traverse.com www.jmurdock.org

  2. Based on the Discovering Algebra Texts–Key Curriculum Press • Investigation-based learning • Appropriate use of technology • Rich and meaningful mathematics • Strong connections to the NCTM Content and Process Standards

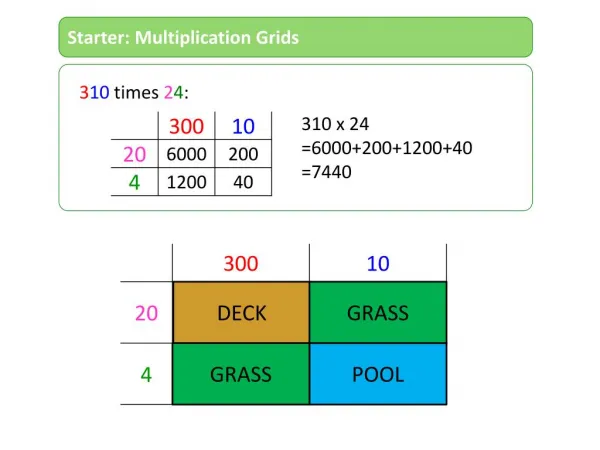
  3. -6.2 ≤ y ≤ 6.2 -9.4 ≤ x ≤ 9.4 Begin by transforming a figure L1 L2 1 1 3 5 5 4 3 3 4 1 We’ll plot this figure in L1 and L2 and the transformed image in L3 and L4.

  4. L3 = L1 – 8, L4 = L2 L3 = L1, L4 = L2 – 6 L3 = L1 – 5, L4 = L2 – 3 Show both original figure and image slide the figure left 8 units. 2. slide the original figure 6 units down. 3. slide the original figure down 3 units and left 5 units.

  5. L3 = L1, L4 = - L2 L5 = - L1, L6 = - L2 L3 = L1 – 5, L4 = 0.5 L2 – 3 Show pre-image and image 4. Reflect figure over the x-axis. Reflect the resulting figure over the y-axis. 6. Shrink the original figure vertically by a factor of 1/2, translate the result 3 units down and left 5 units.

  6. An Explanation •To translate a figure to the left 5 units • New x list = old x list – 5 • To translate a figure to the right 3 units • New x list = old x list + 3 • To slide a figure 6 units down • New y list = old y list – 6 • To reflect a figure over the x-axis • New y list = - (old y list) • To vertically stretch a figure by factor k • New y list = k(old y list)

  7. xpipe.sourceforge.net/ Images/RubicsCube.gif Step by step transformations get the Job done

  8. Create this transformation a solution L3 = - L1 – 3 L4 = - L2 + 4

  9. “I’m very well acquainted, too, with matters mathematical.I understand equations both the simple and quadratical.About binomial theorem I am teeming with a lot of news. . .With many cheerful facts about the square of the hypotenuse!” The Major General’s Song from The Pirates of Penzance by Gilbert and Sullivan

  10. Transformations of Functions -3 -2 -1 1 2 3

  11. Translations of y = x2

  12. Original equation y = x2 • • To move a function to the right 3 units new x = old x + 3 • or old x = new x – 3 • To move a function 3 units right we must replace the old x in the original equation with x – 3.y = (x – 3)2 • Similarly to move a function 2 units left we must replace the old x in the equation with x + 2.y = (x + 2)2 • And to move a function 2 units down we must replace the old y in the equation with y + 2.y + 2 = x2ory = x2 – 2

  13. (-3,5) (1,3) (-2,4) (3,0) Make my graph y = -(x – 1)2 + 3 y = -2(x + 3)2 + 5 y = -(x + 2)2 + 4 y = 0.5(x – 3)2

  14. Don’t tell students the rules! Help them discover the rules!

  15. (-3,5) Write my equation This equation sets the vertex at (-3, 5) y = a(x + 3)2 + 5 Use the point (-2, 3) to determine the value of a 3 = a(-2 + 3)2 + 5 3 = a(1)2 + 5 y = –2(x + 3)2 + 5

  16. Program:CBRSET • Prompt S,N • round (S/N, 5)I • If I > 0.2:-0.25 int(-4I)  I • Send ({0}) • Send ({1, 11, 2, 0, 0, 0}) • Send({3, I, N, 1, 0, 0, 0, 0, 1, 1}) CBR will collect 40 data pairs in 6 seconds

  17. Program:CBRGET • Send ({5,1}) • Get (L2) • Get (L1) • Plot 1 (Scatter, L1, L2, · ) • ZoomStat Program will transfer data from CBR, set window, and plot graph on your calculator

  18. Ask a kid to walk a parabola

  19. A single ball bounce • Set CBR to collect 20 data points during one second. • Drop a ball from a height of about 0.5 meters and trigger the CBR from about 0.5 meters above the ball. Transfer data to all calculators. • Model your parabola with an equation of the form y = a(x – h)2 + k Find a by trial & error or find a by substituting another choice of x and y.

  20. Modeling provides students with • a logical reason for learning algebra- kids don’t ask“When am I ever going to use this?” • Students can gain important conceptual understandings and build up their “bank” of basic symbolic algebra skills. • an integration of algebra with geometry, statistics, data analysis, functions, probability, and trigonometry.

  21. In General identifies the location of the vertex after a translation from (0, 0) to (h, k). This parabola shows a vertical scale factor, a, and horizontal scale factor, b.

  22. Locate your vertex (h, k) • Then find your stretch factors (a & b) by selecting another data point (x1,y1). (h, k) = (0.86, 0.6)

  23. A transformation of y = x2 Choose point (x1,y1) = (1.14, 0.18)

  24. A transformation of y = x2 y = –5.36(x – 0.86)2 + 0.6

  25. (0.9, 0.68) Another bounce example (h, k) = (0.9, 0.68) Choose (x1,y1)= (1.16,1.02)

  26. A symbolic model

  27. A Case for Vertex Form • y = a(x – h)2 + k • Vertex is visible at (h, k) • Easy to approximate the value of a • Supports the order of operations • Easy to solve for x (by undoing)

  28. Evaluate by emphasizing the order of operations • Evaluate this expression when x = 4.5 4.5 3 • Subtract 1.5 9 • Square - 45 • Multiply by –5 - 33 • Add 12 • So, the value of the expression at x = 4.5 is –33

  29. 3 9 –45 –33 An organization template Evaluate this expression when x = 4.5 Operations Results Pick x = 4.5 4.5 – (1.5) ( )2 x (–5) + (12)

  30. 4.5, -1.5 ± 3 9 -45 Solve equations by undoing Results Operations Undo Pick x x = – (1.5) + (1.5) ( )2 ±  x (-5) ÷ (-5) + (12) – (12) -33

  31. Verification! -33 = -5(x – 1.5)2 + 12 when x = -1.5 or 4.5

  32. What question is asked? 5.03(x – 0.9)2 + 0.68 = 1 Operations Undo Result Pick x 1.15…, 0.647… x = – (0.9) + (0.9) ± 0.252… ( )2 ±  0.0636… 0.32 x (5.03) ÷ (5.03) + (0.68) – (0.68) 1

  33. The power of visualization and symbolic algebra

  34. Polynomial  Vertex Form • Use a rectangular model to help complete the square.

  35. Polynomial  Vertex Form • Use a rectangular model to help complete the square.

  36. Verification!

  37. What question is asked? x2 + 12x + 13 = 0 Or (x + 6)2 – 23 = 0 Operations Undo Result Pick x ± (23) – 6 x = + (6) – (6) ± (23) ( )2 ±  23 0 – (23) + (23)

  38. General  Vertex Form • Use a rectangular model to help complete the square.

  39. Vertex is General form and the vertex

  40. An Important Relationship

  41. Rolling Along • Place the CBR at the high end of the table. • Roll the can up from the low end. It should get no closer than 0.5 meters to the CBR. • Collect data for about 6 seconds.

  42. Parab Program

  43. Check out the Transform Program

  44. y = √ (1 – x2)A good function to exhibit horizontal stretches

  45. Paste a picture into Sketchpad

  46. Model with Sketchpad 4

  47. And if the vertex isn’t available? • How about finding a, b, and c by using 3 data pairs? y = ax2 + bx + c

  48. “If we introduce symbolism before the concept is understood, we force students to memorize empty symbols and operations on those symbols rather than internalize the concept.” [Stephen Willoughby, Mathematics Teaching in the Middle School, February 1997, p. 218.]

More Related