1 / 30

Shortest Path in Weighted Graphs Using Matrix Method

This overview discusses the matrix method for finding the shortest path in a weighted graph model. It details steps for constructing a search matrix that represents the graph, including entering path information and calculating path costs efficiently. The presentation outlines how to enter initial data, expand nodes based on the lowest cost entries, and track potential paths until no further nodes can be expanded. The final output showcases the optimized path and its cost, demonstrating how a search tree can be effectively implemented through a matrix structure.

vanna-wilkinson
Télécharger la présentation

Shortest Path in Weighted Graphs Using Matrix Method

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

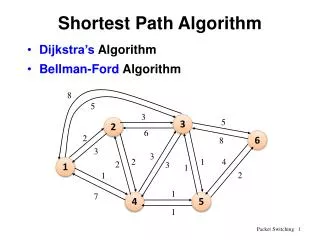
  1. Discrete Math 2Shortest Path Using Matrix CIS112 February 10, 2007

  2. Overview • Previously: • In weighted graph . . • Shortest path from one vertex to another • Search tree method • Now: • Same problem • Matrix method Kutztown University

  3. Strategy • Represent weighted graph as matrix • Create search matrix . . • with entries matching • nodes expansion • node production Kutztown University

  4. Matrix for Weighted Graph Kutztown University

  5. Step #0 • Create a search matrix • Layout same as weighted graph matrix • Entries will hold path information • Vertices along path • Total cost of path • Path info built up step by step Kutztown University

  6. Search Matrix Kutztown University

  7. Step #1 • Enter information for first path segment • Initial entry goes in row #7 . . • Since #7 is starting vertex Kutztown University

  8. Search Matrix – Step #1 Kutztown University

  9. Comment • Notice similarity to search tree • Choose lowest cost entry • Which is in column #3 • Corresponds to expanding lowest cost node • Next entry goes in row #3 Kutztown University

  10. Search Matrix – Step #2 Kutztown University

  11. Comment • Entries represent path cost • 15+8=23 • 15+19=34 • Path elements stored implicitly • Look in row #7 (starting point) • Find lowest cost entry (column #3) • In corresponding row • Find lowest cost entry (column #1) • Path is: 7  1 • Again, note similarity to search tree Kutztown University

  12. Step #3 • Among all leaves . . • Find lowest cost entry [7,10] • “Expand” “node” #10 • I.e., compute path cost + edge cost • Enter into matrix Kutztown University

  13. Search Matrix – Step #3 Kutztown University

  14. Comment • No entry is made for starting point – #7 • There are two entries in column #8 • Correspondence to search tree • Two nodes for #8 • So we mark higher one as deleted Kutztown University

  15. Search Matrix – Step #3b Kutztown University

  16. Continuing . . • Keep choosing “nodes” • Keep “expanding” them • Until there are no more to “expand” Kutztown University

  17. Search Matrix – Step #4 Kutztown University

  18. Search Matrix – Step #4b Kutztown University

  19. Comment • Reached #12, but not yet finished • Other less costly path possible • But not through #4 & #9 • Why not? • So mark #4 & #9 as dead ends Kutztown University

  20. Search Matrix – Step #4c Kutztown University

  21. Step #5 • Now expand #1 . . • Marking dead ends, if they occur Kutztown University

  22. Search Matrix – Step #5 Kutztown University

  23. Comment • All entries in row #1 are dead ends • So the column is also a dead end • Then the same happens . . • with row #3 • and column #3 Kutztown University

  24. Search Matrix – Step #5b Kutztown University

  25. Step #6 • And expand #8 . . • Marking dead ends, if they occur Kutztown University

  26. Search Matrix – Step #6 Kutztown University

  27. Comment • We are finished . . • since there are no more nodes to expand • We already have the path cost = 26 • How do we get the path? Kutztown University

  28. To Get the Path • Start at row 7 • Column 10 has an entry . . • giving us 7  10 • Go to row 10 • Column has 11 an entry . . • giving us 7  10  11 • Go to row 11 • Column has 12 an entry . . • giving us 7  10  11  12 Kutztown University

  29. Shortest Path from 7 to 12 • 7  10  11  12 :: 26 Kutztown University

  30. Final Comments • We see how the 1-1 search tree can be implemented as a matrix • We look next at how the 1-many can also Kutztown University

More Related