1 / 14

Atomic Physics Selected Topics - 2

Atomic Physics Selected Topics - 2. The Bohr Model of the Atom. In 1913 Neils Bohr provided an explanation of atomic spectra that includes some features of the currently accepted theory. His model included both classical and non-classical ideas.

wmcclure
Télécharger la présentation

Atomic Physics Selected Topics - 2

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Atomic Physics Selected Topics - 2

  2. The Bohr Model of the Atom In 1913 Neils Bohr provided an explanation of atomic spectra that includes some features of the currently accepted theory. His model included both classical and non-classical ideas. His model included an attempt to explain why the atom was stable.

  3. Assumptions for Hydrogen • The electron moves in circular orbits around the proton under the influence of the Coulomb force of attraction. • The Coulomb force produces the centripetal acceleration.

  4. Assumptions for Hydrogen • Only certain electron orbits are stable. • These are the orbits in which the atom does not emit energy in the form of electromagnetic radiation. • Therefore, the energy of the atom remains constant and classical mechanics can be used to describe the electron’s motion.

  5. Assumptions for Hydrogen • Radiation is emitted by the atom when the electron “jumps” from a more energetic initial state to a lower state. • The “jump” cannot be treated classically.

  6. Assumptions for Hydrogen • The frequency emitted in the “jump” is related to the change in the atom’s energy. • It is generally not the same as the frequency of the electron’s orbital motion. • The frequency is given by Ei – Ef = hƒ • The size of the allowed electron orbits is determined by a condition imposed on the electron’s orbital angular momentum.

  7. Assumptions for Hydrogen • Angular momentum is “quantized.” This condition is based on Bohr’s Correspondence Principle: quantum mechanics is in agreement with classical physics when the energy differences between quantized energy levels are very small. • This is similar to having Newtonian Mechanics be a special case of relativistic mechanics when u << c.

  8. The electron’s orbital angular momentum is • meur = nħ • where n = 1, 2, 3, … • The total energy of the atom is • The energy of the atom can also be expressed as

  9. The radii of the Bohr orbits are quantized: • This is based on the assumption that the electron can only exist in certain allowed orbits determined by the integer n. • When n = 1, the orbit has the smallest radius, called the Bohr radius, ao. • ao = 0.0529 nm

  10. A general expression for the radius of any orbit in a hydrogen atom is • rn = n2ao • The energy of any orbit is • En = - 13.6 eV/ n2

  11. The lowest energy state is called the ground state. • This corresponds to n = 1. • Ground state energy is –13.6 eV. • The next energy level has an energy of –3.40 eV. • The energies can be compiled in an energy level diagram.

  12. The ionization energy is the energy needed to completely remove the electron from the atom. The ionization energy for hydrogen is 13.6 eV. The uppermost level corresponds to E = 0 and n .

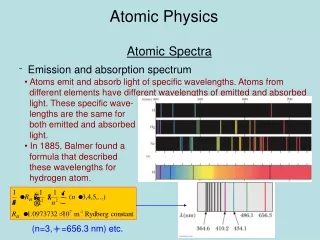
  13. Energy Level Diagram The value of RH from Bohr’s analysis is in excellent agreement with the experimental value. A more generalized equation can be used to find the wavelengths of any spectral lines.

  14. The wavelengths of hydrogen’s spectral lines can be found from • RH is the Rydberg constant. • RH = 1.097 373 2 x 107 m-1. • nf < ni (integers) • The visible spectral lines correspond to • nf= 2, ni = 3, 4, 5, 6.

More Related