Limits and continuity

1. Limits and continuity

2. Start from an example • If the voltage apply to the resistor can be express by the function Determine the maximum voltage across the resistor. • We can calculate the maximum or minimum by use derivative

3. Contents • Concepts of Limits and Continuity • Derivatives of functions • Differentiation rules and Higher Derivatives • Applications

4. Differential Calculus Concepts of Limits and Continuity

5. The idea of limits • Consider a function • The function is well-defined for all real values of x • The following table shows some of the values:

6. The idea of limits

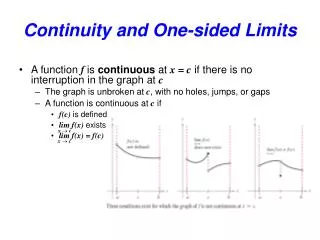
7. Concept of Continuity E.g. is continuous at x=3? The following table shows some of the values: • exists as and • => f(x) is continuous at x=3!

8. Differential Calculus Derivatives of functions

9. y Y=f(x) f(x0+Dx) B Dy A C f(x0) Dx x0 x0+Dx Derivative (導數) • Given y=f(x), if variable x is given an increment Dx from x=x0, then y would change to f(x0+Dx) • Dy= f(x0+Dx) – f(x) • Dy/Dx is the slope of triangular ABC x

10. Derivative • What happen with Dy/Dx as Dx tends to 0? • It seems that Dy/Dx will be close to the slope of the curve y=f(x) at x0. • We defined a new quantity as follows • If the limit exists, we called this new quantity as the derivative of f(x). • The process of finding derivative of f(x)is called differentiation.

11. Y=f(x) f(x0+Dx) B Dy A C f(x0) Dx x x0 x0+Dx Derivative y Derivative of f(x) at Xo = slope of f(x) at Xo

12. Differentiation from first principle Find the derivative of with respect to (w.r.t.) x To obtain the derivative of a function by its definition is called differentiation of the function from first principles

13. Differential Calculus Differentiation rules and Higher Derivatives

14. Fundamental formulas for differentiation I • Let f(x) and g(x) be differentiable functions and c be a constant. for any real number n

15. Examples • Differentiate and w.r.t. x

16. Fundamental formulas for differentiation II • Let f(x) and g(x) be differentiable functions

17. Example 1 Differentiate w.r.t. x

18. Example 2 Differentiate w.r.t. x

19. Fundamental formulas for differentiation III ln(x) is called natural logarithm

20. Differentiation of composite functions • To differentiate w.r.t. x, we may have problems as we don’t have a formula to do so. • The problem can be simplified by considering composite function: Let so and

21. Chain Rule Chain Rule states that : given y=g(u), and u=f(x) So our problem and

22. Example 1 Differentiate w.r.t. x Simplify y by letting so now By chain rule

23. Example 2 Differentiate w.r.t. x Simplify y by letting so now By chain rule

24. Example 3 Differentiate w.r.t. x Simplify y by letting so now By chain rule

25. Higher Derivatives) • If the derivatives of y=f(x) is differentiable function of x, its derivative is called the second derivative of y=f(x) and is denoted by or f ’’(x). That is • Similarly, the third derivative = • the n-th derivative =

26. Example • Find if

27. Differential Calculus Applications

28. Y=f(x) f(x0+Dx) B Dy A C f(x0) Dx x x0 x0+Dx Slope of a curve • Recall that the derivative of a curve evaluate at a point is the slope of the curve at that point. Derivative of f(x) at Xo = slope of f(x) at Xo

29. Slope of a curve • Find the slope of y=2x+3 at x=0 • To find the slope of a curve, we have to compute the derivative of y and then evaluate at a point • The slope of y at x=0 equals 2 (y=mx+c now m=2)

30. Slope of a curve • Find the slope of at x=0, 2, -2 • The slope of y = 2x • The slope of y (at x=0) = 2(0) = 0 • The slope of y (at x=-2) =2(-2) = -4 • The slope of y (at x=2) =2(2) = 4 X=-2 X=2 X=0

31. D B X1 C X2 A Local maximum and minimum point • For a continuous function, the point at which is called a stationary point. • This gives the point local maximum or local minimum of the curve

32. First derivative test (Max) Given a continuous function y=f(x) If dy/dx = 0 at x=xo & dy/dx changes from +ve to –ve through x0, x=x0 is a local maximum point local maximum point x=x0

33. First derivative test (Min) Given a continuous function y=f(x) If dy/dx = 0 at x=xo & dy/dx changes from -ve to +ve through x0, x=x0 is a local minimum point x=x0 local minimum point

34. Example • Determine the position of any local maximum and minimum of the function First, find all stationary point (i.e. find x such that dy/dx = 0) , so when x=0 By first derivative test x=0 is a local minimum point

35. Example 2 Find the local maximum and minimum of Find all stationary points first:

36. Example 2 By first derivative test, • x=1 is the local maximum (+ve -> 0 -> -ve) • x=3 is the local minimum (-ve -> 0 -> +ve)

37. Second derivative test Second derivative test states: • There is a local maximum point in y=f(x) at x=x0, if at x=x0 and < 0 at x=x0. • There is a local minimum point in y=f(x) at x=x0, if at x=x0 and > 0 at x=x0. • If dy/dx = 0 and =0 both at x=x0, the second derivative test fails and we must return to the first derivative test.

38. Example Find the local maximum and minimum of Find all stationary points first: By second derivative test, x=1 is max and x=3 is min

39. x