1 / 20

Continuity and One Sided Limits

Section 2.4. Continuity and One Sided Limits. Continuity. To say a function is continuous at x = c means that there is NO interruption in the graph of f at c. The graph has no holes, gaps, or jumps. Breaking Continuity. 1. The function is undefined at x = c. Breaking Continuity. 2.

shepry
Télécharger la présentation

Continuity and One Sided Limits

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Section 2.4 Continuity and One Sided Limits

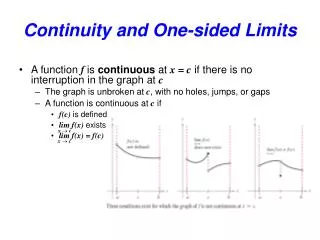
  2. Continuity • To say a function is continuous at x = c means that there is NO interruption in the graph of f at c. The graph has no holes, gaps, or jumps.

  3. Breaking Continuity • 1. The function is undefined at x = c

  4. Breaking Continuity • 2.

  5. Breaking Continuity • 3.

  6. Definition of Continuity • A function f is continuous at c IFF ALLare true… • 1. f(c) is defined. • 2. • 3. • A function is continuous on an interval (a, b) if it is continuous at each pt on the interval.

  7. Discontinuity • A function is discontinuous at c if f is defined on (a, b) containing c (except maybe at c) and f is not continuous at c.

  8. 2 Types of Discontinuity • 1. Removable : • You can factor/cancel out, therefore making it continuous by redefining f(c). • 2. Non-Removable: • You can’t remove it/cancel it out!

  9. Examples: • 1. Removable: • We “removed” the (x-2). • Therefore, we have a REMOVABLE DISCONTINUITY when x – 2 = 0, or, when x = 2.

  10. Non-Removable: • We can’t remove/cancel out this discontinuity, so we have a NON-Removable discontinuity when x – 1 =0, or when x = 1. • We will learn that Non-Removable Discontinuities are actually Vertical Asymptotes!

  11. To Find Discontinuities… • 1. Set the deno = 0 and solve. • 2. If you can factor and cancel out (ie-remove it) you have a REMOVABLE Discontinuity. • 3. If not, you have a NON-Removable Discontinuity.

  12. One Sided Limits • You can evaluate limits for the left side, or from the right side.

  13. Limits from the Right • x approaches c from values that are greater than c.

  14. Limits from the Left • x approaches c from values that are less than c.

  15. Find each limit… • 1. = 0

  16. 2. = 1 = -1 Therefore, the limit as x approaches 0 DNE!!

  17. 3. 3 3 3

  18. Steps for Solving One Sided Limits • 1. Factor and cancel as usual. • 2. Evaluate the resulting function for the value when x=c. • 3. If this answer is NOT UNDEFINED then that is your solution. • 4. If this answer is UNDEFINED, then graph the function and look at the graph for when x=c.

  19. Steps for Solving a Step Function • Ex: • Evaluate each function separately for the value when x=c. • If the solutions are all the same, that is your limit. • If they are not, then the limit DNE.

  20. = 1 Therefore, the limit as x approaches 1 of f(x) =1 = 1

More Related