1 / 20

Understanding Truth Tables: Conjunctions, Disjunctions, and Compound Statements

Dive into the intriguing world of truth tables, essential for evaluating compound statements in logic. This guide will explore the concepts of conjunctions and disjunctions, highlighting their distinct definitions, symbols, and truth conditions. Conjunctions, represented by "and" (^) are true only when all components are true, while disjunctions, denoted by "or" (v), are true if at least one component is true. Discover how to create and analyze truth tables, including examples, to deepen your understanding of tautologies and contradictions.

zaide
Télécharger la présentation

Understanding Truth Tables: Conjunctions, Disjunctions, and Compound Statements

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Notes - Truth Tables fun, fun, and more fun!!!! 

  2. A compound statement • is created by combining two or more statements, p and q.

  3. Conjunction • uses the word “ and” • Symbol ^ • True only when all parts are true

  4. Disjunction • uses the word “or” • Symbol v • True if any one of its parts are true

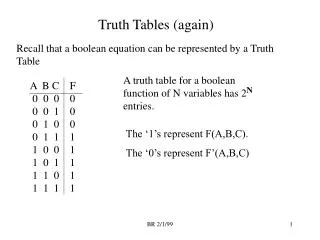
  5. truth table • a table that lists all possible combinations of truth values • ****Be sure to include all possible combinations of truth values for each piece of the compound statement***

  6. Conjunction

  7. Disjunction

  8. Negation

  9. A statement whose truth table contains only True in the final column is a tautology • A statement whose truth table contains only False in the final column is a contradiction

  10. Conditional – think only time false is a broken promise

  11. Example 1.~(p v q)

  12. Example 1.~(p v q)

  13. Example 2.p ^ ~q

  14. Example 2.p ^ ~q

  15. Ex 3.(p ^ q) q

  16. Ex 3.(p ^ q) q

  17. Ex 4.(p v q) ~p

  18. Ex 4.(p v q) ~p

  19. (p ^ q) v (p ^ r)

  20. (p ^ q) v (p ^ r)

More Related