1 / 10

Understanding Truth Tables: Determining Tautologies, Contradictions, and Equivalences

Explore the essential uses of truth tables in logic. Learn to identify truth conditions for compound statements, ascertain if statements are tautologies, contradictions, or neither. Discover how to determine the equivalence of two logical formulas by comparing their truth values. The guide includes clear instructions for constructing truth tables, testing for logical equivalence, and emphasizes the importance of negation distribution. Gain a solid understanding of logical relationships and enhance your analytical skills with truth tables.

candra
Télécharger la présentation

Understanding Truth Tables: Determining Tautologies, Contradictions, and Equivalences

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

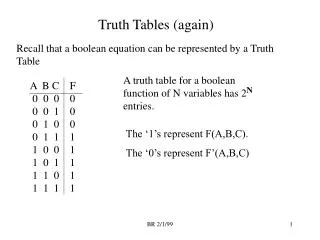
  1. Uses for Truth Tables • Determine the truth conditions for any compound statement • Determine whether a statement is a tautology, a contradiction or neither, • Determine whether two formulae are equivalent.

  2. Equivalence • Two formulae are said to be equivalent if, but only if, those formulae are true and false under exactly the same conditions, that is, if, but only if, the truth table columns for the dominant operators are identical.

  3. Testing for Equivalence • To use a truth table to test two formulae for equivalence, begin by constructing truth table columns for each formula. Use one set of guide columns for both formulae. • Compare the columns for the dominant operators of the two formulae. If the truth values agree in each row, the formulae are equivalent.

  4. Truth-Table Test for Equivalence ( R  S ) :: ~ R  S T T T  T T T T  F  T    T T T  T T  T F T  T  Do the formulas match in truth value? YES Are the two formulas logically equivalent? YES

  5. Truth-Table Test for Equivalence ~ ( R  S ) :: ~ R  ~ S  T T T  T   T T T    T  T  T   T T    T T    T  T T  Do the formulas match in truth value? NO Are the two formulas logically equivalent? NO

  6. Truth-Table Test for Equivalence ~ ( R  S ) :: ~ R  ~ S  T T T  T   T T T    T T T  T   T T  T  T T    T  T T  Do the formulas match in truth value? YES Are the two formulas logically equivalent? YES

  7. Truth-Table Test for Equivalence ~ ( R  S ) :: ~ R  ~ S  T T T  T   T  T T   T T T    T T T  T  T T    T  T T  Do the formulas match in truth value? NO Are the two formulas logically equivalent? NO

  8. Truth-Table Test for Equivalence ~ ( R  S ) :: ~ R  ~ S  T T T  T   T  T T   T  T    T T T    T T    T  T T  Do the formulas match in truth value? YES Are the two formulas logically equivalent? YES

  9. Do Not Distribute a Negation Across A Conjunction or a Disjunction! not ( R and S)  not R andnot S not ( R or S)  not R ornot S

  10. Rather. . . not R ornot S not ( R and S) = not ( R or S) = not R andnot S

More Related