Edge Detection by applying the Marr-Hildreth detector

2. Seminar MPEG4 with TSSA Edge Detectionby applying theMarr-Hildreth detector Bastian Schulz february 2001

3. Edge Detection Topics • 1. Introduction • 2. Finding edges • 3. Handling noise • 4. Marr-Hildreth detector • 5. My implementation on TriMedia • 6. Results

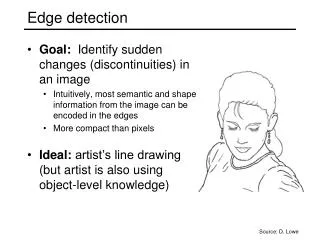
4. Edge Detection 1. Introduction • Why edge detection? • Sharpen an image (f.inst. in Photoshop) • Identifying objects in scenes reducing amount of data in video sequences  classifying of images by its content

5. Edge Detection 1. Introduction • Difficulties • Several kinds of edges • 1: different distances • edge at object • 2: different distance • no edge at object • 3: continous distance • edge at object • 4: shadows • 5: change of color • or reflectance • Noise

6. Edge Detection 2. Finding edges   • Edge  large variation of intensity function f(x) • Steepness of a function  1st derivative f ‘(x) • Finding edges  finding max + min of f ‘(x) • Or: finding zero crossings of the 2nd derivative f ‘‘(x)

7. Edge Detection 2. Finding edges Discrete derivatives

8. Edge Detection 2. Finding edges Discrete derivatives Second discrete derivative: Dx2f Dx2f = Dx (Dx f ) = Dx (f(x+1,y) - f(x,y) ) = [ f(x+1+1,y) - f(x+1,y) ] - [ f(x+1,y) - f(x,y) ] = f (x+2,y) - 2f (x+1,y) + f (x,y)

9. Edge Detection 3. Handling noise • Now: I(x,y) + N(x,y)  J(x,y) • Image Noise disturbed Image • Noise is placed in the higher frequencies •  applying a low-pass filter (smoothing the image) would eleminate the noise. • Tradeoff problem: • Smoothing J(x,y) too much changes the original image I(x,y) • Smoothing not enough keeps the noise N(x,y)

10. Edge Detection 4. Marr-Hildreth detector • Common filters • Band-limited filters  infinite impulse responses in spatial domain • FIR filter (finite impuls response)  infinite frequency support in frequency domain • Best compromise between these two solutions: • the class of the Gaussian functions

11. Edge Detection 4. Marr-Hildreth detector Marr-Hildreth detector uses a Gaussian filter to smooth the image G(x) = (2 2)-½ exp(-x2/2 2) D2G(x) = - (2)-½ -3(1 - x2/ 2)exp(-x2/2 2) The functionD2G(x) in spatial and Fourier domain

12. Edge Detection 4. Marr-Hildreth detector • Marr-Hildreth detector • After convolving the image function f(x,y) with D2G(x) • Search the zero crossings of the result • Compute the first derivative DG(x)  f(x,y) at these points • DG(x)  f(x,y) > Threshold T  point belongs to edge • DG(x)  f(x,y) < Threshold T  edge not steep enough

13. Edge Detection 5. My implementation • input.yuv loaded in one frame to input buffer • discrete convolution of every pixel • for all pixels with -1 < D2G(x)  f(x,y) < 1 if DG(x)  f(x,y) > Threshold T pixel is black • else: pixel is white • write a black or white pixel in the output buffer

14. Edge Detection 5. My implementation • Possible Extensions • searches only in the Y-frame of the YUV-image (black/white) • computes derivatives in stationary directions ( x and y ) • constant parameter  of 2, the values of DG(x) and D2G(x) are fixed

15. Edge Detection 6. Results What is it? Sigma  = 2, Threshold (for 1st derivative) = 3 size of the image: 290x200 pixel Computing time: 5 min 02 sec ? 

16. Edge Detection 6. Results Who is it? Sigma  = 2, Threshold (for 1st derivative) = 3 size of the image: 200x200 pixel Computing time: 3 min 09 sec  ?

17. THE END