All-Pairs Shortest Paths
200 likes | 517 Vues
All-Pairs Shortest Paths. Problem Given a graph G = ( V , E ), where every edge e has weight w ( e ), find, for every pair of vertices u , v in V , a shortest path from u to v. Input: an adjacency matrix. Output in tabular form : the entry in u ’s row and v ’s

All-Pairs Shortest Paths
E N D
Presentation Transcript
All-Pairs Shortest Paths ProblemGiven a graph G = (V, E), where every edge e has weight w(e), find, for every pair of vertices u, v in V, a shortest path from u to v. Input: anadjacency matrix. Output intabular form: the entry in u’s row and v’s column is the length of the shortest path from u to v. Negative weights allowed. (Dijkstra’s algorithm no longer applicable.) No negative-weight cycles.
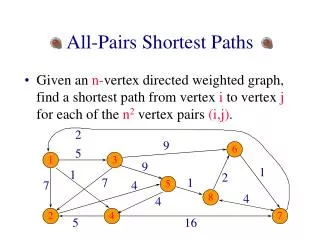
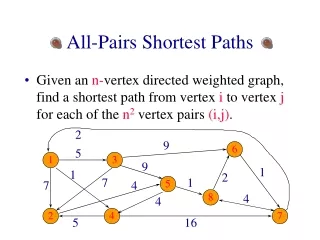
n n matrix W = (w ) where ij 0 if i = j w = weight of (i, j) if i j & (i, j) in E otherwise ij 0 3 8 -4 0 1 7 4 0 2 -5 0 6 0 An Example Input 2 4 3 8 3 1 7 1 2 -4 -5 5 4 6
Path: 1- 5 - 4 - 3 - 2 = – 4 + 6 – 5 + 4 4 - 1- 5 5 - 4 - 1 Cont’d Output 2 4 3 8 3 1 0 1 -3 2 -4 3 0 -4 1 -1 7 4 0 5 3 2 -1 -5 0 -2 8 5 1 6 0 7 1 2 -4 -5 5 4 6
(m) d = weight of shortest path from i to j that uses at most m edges ij 0 if i = j if i j (0) d = ij k’s (k≠ i, j) m 1 edges m 1 edges A Recursive Definition i j
(m-1) (m) d = min { d + w } ij ik kj 1 k n for k 1 ton do ifd > d + w thend d + w k’s ij ik kj ij ik kj m 1 edges i j (n 1) (n) (n+1) no cycle on a shortest path d = d = d = ... m 1 edges ij ij ij Relaxation (k≠ i, j) Length of the shortest path from i to j is
(n – 1) (1) 3 n 1 calls to ESP to compute D , …, D , each taking (n ). 4 (n )total time Dynamic Programming (l) (l) (l – 1) Extend-Shortest-Paths(n,W) // compute D = (d ) from D let D = (d ) be an nn matrix fori 1 ton do forj 1 ton dod fork 1 ton dod min (d , d + w ) returnD ij ij ij ij ij ik kj
j = 1, …, n d = min (d , d+ w ) ij ij ik kj d = d+dw ij ij ik kj (m) (m – 1) As if D = D “” W m = 1, …, n –1 where 0 … 0 … … … 0 (0) D = (n – 1) n – 1 And D = W contains the shortest-path weights. Matrix Multiplication Extend-Shortest-Paths( ) is similar to matrix multiplication: correspondence
Repeated squaring 2kkk W = WW Compute lg(n 1) 2 4 2 W, W , W , … W lg(n 1) + 1 3 (n lg n)time: (lg n) squarings each squaring (n ) time 3 An Improvement
(m) d = weight of a shortest path from i to j with intermediate vertices in { 1, 2, …, m }. ij i mm m ... j (n) Then the length of shortest path from i to j is d ij Floyd-Warshall Algorithm Even faster by a factor of lgn!
(0) d = w i j ij ij (k) (k-1) (k-1) (k-1) d = min ( d , d + d ) if k 1 ij ij ik kj (k-1) (k-1) d d k kj ik j i (k-1) d ij Recursive Definition of d
The Procedure Floyd-Warshall(n, W) DW fork 1 ton do fori 1 ton do forj 1 ton d min (d , d + d ) returnD (0) (k) (k-1) (k-1) (k-1) ij ij ik kj (n) 3 Running time (n )!
(k) j i ij (0) = ij (k-1) (k-1) (k-1) (k-1) if d d + d ij kj ij ik (k) = i ij (k-1) j otherwise kj k Constructing Shortest Paths (k) (k) Predecessor matrix = ( ) : ij shortest path from i to j with all intermediate vertices in {1, 2, …, k}. i, if (i, j) E NIL, if (i, j) E
0 3 5 0 1 6 0 2 4 0 (0) D (0) NIL 1 1 NIL NIL NIL 2 2 NIL NIL NIL 3 4 NIL NIL NIL 0 3 5 0 1 6 0 2 4 79 0 (1) NIL 1 1 NIL NIL NIL 2 2 NIL NIL NIL 3 4 11 NIL (1) D An Example 3 1 2 1 5 6 2 3 4 4 With 1 as a possible intermediate vertex:
0 3 49 0 1 6 0 2 4 7 8 0 NIL 1 2 2 NIL NIL 2 2 NIL NIL NIL 3 412 NIL (2) (2) D 0 3 4 6 0 1 3 0 2 4 7 8 0 NIL 1 2 3 NIL NIL 2 3 NIL NIL NIL 3 4 1 2 NIL (3) (3) D NIL 1 2 3 4 NIL 2 3 4 1 NIL 3 4 1 2 NIL 0 3 4 6 7 0 1 3 69 0 2 4 7 8 0 (4) (4) D An Example (cont’d)
An Example (cont’d) 4 3 2 1 2 3 4 1 2 4 3 3 1 1 2 3 3 4 1 2 2 2 3 1 1 3 4 2 3 4
Transitive Closure Thetransitive closureof a graph G = (V, E) is G* = (V, E*) such that (i, j) E* iff there is a path from i to j in G. G*: G: 1 1 5 2 2 5 3 4 3 4
1 if i = j or an edge between vertices i and j entry (i , j) = 0 otherwise if i j Floyd-Warshall algorithm, replacing x y min boolean OR + boolean AND i j 3 Running time(n ) Solution: Floyd-Warshall Adjacency matrix is initialized as (weights not needed) AND AND OR OR