Introduction to Probability : Binomial & Normal Distribution

1. Introduction to Probability : Binomial & Normal Distribution Dr. Marvin Reid

2. Objectives • Define probability and its importance in statistical theory • Describe the associative and multiplicative rules for joint probability under statistical independence • Describe the properties and uses of 2 probability distribution functions the normal & binomial distributions.

3. Review • Populations • samples drawn from these populations • Methods used to summarize the data obtained from these samples • The relation between sample and population is uncertain. Thus to make inferences about our data we need to set up mathematical models which capture this uncertainty • The foundation of statistical models is probability theory

4. Probability • Relative frequency • Degree of belief • Probability reasons from the population to the sample • Probability lies between 0 and 1

5. Definitions • Trial (Experiment) – any process generates a set of results • Outcome – the result of carrying out the trial • Event – one or more outcomes • Marginal probability –one event occurs

6. Joint conditions • Mutually exclusive if the events cannot occur simultaneously • Independent if the occurrence of an event does not influence the probability of another event occurring

7. Start No Addition Rule P(A or B)=P(A)+P(B)-P(AB) Are events mutually exclusive yes Addition Rule P(A or B)=P(A)+P(B) Joint Probability P(AB)=P(A) x P(B) Are events statistically independent yes Marginal Probability P(A)

8. Probability distributions • Many statistical methods use probability distribution • Probability distribution is used to calculate the theoretical probability of different values occurring • Normal distribution – continuous data • Binomial distribution- discrete data

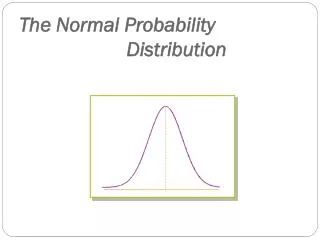
9. Normal Distribution • Extends from –infinity to +infinity • Height=probability density • Area under curve=1 • Unimodal • mean=median=mode

10. y1;µ=50;σ=5 y2;µ=50;σ=10 Normal distribution-variation with sd Completely described by the mean & sd

11. Standard Normal Distribution Any normally distributed variable can be related to the standard normal distribution whose mean is zero and standard deviation is 1. This can be done by performing the following calculation Z is the distance along the x axis in sd units

12. Some uses of Normal Distribution 95% • Used to calculate probability of values being within specified range eg 95%CI= m ± (1.96 x se) • Used to test inferences about the difference between a single mean and a hypothesized value and the difference between two means

13. The Binomial Distribution • Describes discrete data resulting from experiments called Bernoulli process • Each experiment (trial) has only 2 possible outcomes. • The probability of the outcome of any trial remains fixed over time. • The trials are statistically independent. • Example = Toss of fair Coin

14. Binomial Formula • p=probability of success • q=(1-p)=probability of failure • r=number of successes desired • n=number of trials undertaken Binomial Formula

15. Problem • A couple each with sickle trait have 4 children. What is the probability that two children will have sickle cell disease. • P(SS)=0.25, q(Non-SS)=0.75, n=4.

16. Calculations

17. Calculation with Excel

18. Characteristics of the Binomial Distribution • When p is small the binomial distribution is skewed to the right • As p increases the skewness is less noticeable • When p=.5 the binomial distribution is symmetrical • When p >0.5 the distribution is skewed to the left • As n increases binomial distribution approximates the normal distribution (np and nq>5)

19. Family of Binomial Distribution P=0.1 P=0.5 P=0.7 P=0.4

20. Binomial statistics Mean of a Binomial Distribution Standard Deviation of a Binomial Distribution Standard error of the proportion

21. Some uses of the Binomial distribution • Used to calculate probability of values being within specified range eg CI • Used to test inferences about the difference between a single proportion and a hypothesized value and the difference between two proportions

22. Calculating interval estimates of the proportion from large samples Z is the appropriate percentage point of the normal distribution

23. Example • Dr. McGaw-Binns surveyed 150 medical students and found that 42% of them had a sedentary lifestyle • A) Estimate the standard error of the proportion • B) Construct a 95% confidence interval for the true proportion of students who had a sedentary lifestyle

24. Solution to example N=150, p=0.42

25. Solution with stata • The stata command • cii number probability • cii 150 0.42 -- Binomial Exact -- Variable | Obs Mean Std. Err. [95% Conf. Interval] -------------+------------------------------------------------------------- | 150 .42 .0402989 .3399811 .503244

26. Comparing two proportions • p1 and p2 are the proportions • se=standard error • p=overall proportion based on the two sample proportions Compare calculated z with the appropriate percentage point Zαof the normal distribution appropriate

27. Objectives • Define probability and its importance in statistical theory • Describe the associative and multiplicative rules for joint probability under statistical independence • Describe the properties and uses of 2 probability distribution functions the normal & binomial distributions.