1 / 35

3.Gate-Level Minimization

3.Gate-Level Minimization. Gate-Level Minimization – Two-Variable Map. xyz + xyz' = xy(z+z')=xy xyz + xy'z = x(y+y')z=xz xyz + x'yz = (x+x')yz=yz  인접항들의 결합임 xyz + x'y'z ‘ = ? (minimization 안됨 ) 즉 분배법칙을 통한 minimization 과정  인접항들을 찾는 과정 필요함 하나의 minterm 은 3 개의 인접항들을 갖음.

danno
Télécharger la présentation

3.Gate-Level Minimization

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

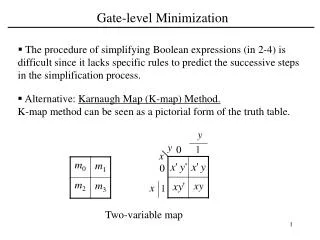
  1. 3.Gate-Level Minimization

  2. Gate-Level Minimization –Two-Variable Map • xyz + xyz' = xy(z+z')=xy • xyz + xy'z = x(y+y')z=xz • xyz + x'yz = (x+x')yz=yz  인접항들의 결합임 • xyz + x'y'z‘ = ? (minimization 안됨) • 즉 분배법칙을 통한 minimization 과정  인접항들을 찾는 과정 필요함 • 하나의 minterm 은 3개의 인접항들을 갖음

  3. Gate-Level Minimization –Two-Variable Map

  4. Gate-Level Minimization –Two-Variable Map 빈 칸 채워볼 것

  5. Gate-Level Minimization –Two-Variable Map • m1+m2+m3 = x'y +xy' +xy = x(y+y’) + y(x+x’) = x +y • Two-Variable Map • Three-Variable Map –위치 암기하기

  6. Gate-Level Minimization –Three-Variable Map • Map 에서 인접셀은 변수중 하나만 complement 관계이고 나머지는 같은 변수로 이루어짐 • m0와 m4의 차이점? m0 + m4 = ? • m1와 m3의 차이점? m1 + m3= ? • m6와 m4의 차이점? m6 + m4= ? • m0 + m1 + m4 + m5= ?

  7. Gate-Level Minimization –Three-Variable Map • Ex 3-1) Simplify the Boolean function, F(x, y, z) = Σ(2, 3, 4, 5) F = x'y + xy' • Ex 3-2) F(x, y, z) = Σ(3,4,6,7) F = yz+xz'

  8. Gate-Level Minimization –Three-Variable Map • Ex 3-3) Simplify the Boolean function, F(x, y, z) = Σ(0,2,4,5,6) F = z'+xy' • Ex 3-4) Given Boolean function, F = A'C + A'B +AB'C +BC a) express it in sum of minterms F(A, B, C) = Σ(1, 2, 3, 5, 7) b) find the minimal sum of products F = C + A'B 위의 2개의 example 해볼 것

  9. Gate-Level Minimization –Four-Variable Map Ex 3-5) Simplify the Boolean function, F(w, x, y, z) = Σ(0, 1, 2, 4, 5, 6, 8, 9, 12, 13, 14) F = y'+ w'z' + xz' Ex 3-6) 해볼 것 1

  10. Gate-Level Minimization –Prime Implicants • F(A,B,C,D) = Σ(0,2,3,5,7,8,9,10,11,13,15) F=BD+B'D'+CD+AD =BD+B'D'+CD+AB' =BD+B'D'+B'C+AD =BD+B'D'+B’C+AB'

  11. Gate-Level Minimization –Five-Variable Map *순서 외울것

  12. Gate-Level Minimization –Five-Variable Map • Ex 3-7) Simplify the Boolean function, F(A,B,C,D,E)=Σ(0,2,4,6,9,13,21,23,25,29,31) F = A'B'E' + BD'E + ACE * 위의 예제 해볼 것

  13. Product of Sums Simplification • Ex 3-8) Simplify the Boolean function, F(A, B, C, D) = Σ(0, 1, 2, 5, 8, 9, 10) a) sum of products F = B'D' + B'C' +A'C'D b) product of sum F = (A' +B')(C' +D')(B' +D)

  14. Product of Sums Simplification • Ex 3-8) Simplify the Boolean function, F(A, B, C, D) = Σ(0, 1, 2, 5, 8, 9, 10) b) product of sum G=F' = AB + CD + BD' F = G'=(A' +B')(C' +D')(B' +D)

  15. Product of Sums Simplification • F( x, y, z) = Σ(1, 3, 4, 6) = ∏(0, 2, 5, 7) F = x'z +xz' F' = xz +x'z' F = (x'+z')(x + z) * 위의 예제 해 볼 것

  16. Don’t-Care Conditions x y F 0 0 1 0 1 0 1 0 0 1 1 1 x y F 0 0 1 0 1 1 1 0 0 1 1 1 x y F 0 0 1 0 1 X 1 0 0 1 1 1 1 0 0 1 1 1 0 1 1 X 0 1 F = x’y’ + xy F = x’ + y F = x’ + y

  17. Don’t-Care Conditions x y F 0 0 1 0 1 0 1 0 1 1 1 0 x y F 0 0 1 0 1 1 1 0 1 1 1 0 x y F 0 0 1 0 1 X 1 0 1 1 1 0 1 0 1 0 1 1 1 0 1 X 1 0 F = y’ F = x’ + y’ F = y’

  18. Don’t-Care Conditions • Ex 3-9) Simplify the Boolean function, F(w, x, y, z) = Σ(1,3,7,11,15) Don’t-care conditions, d(w, x, y, z) = Σ(0, 2, 5) F(w, x, y, z) = yz + w'x' = Σ(0, 1, 2, 3, 7, 11, 15) F(w, x, y, z) = yz + w'z = Σ(1, 3, 5, 7, 11, 15)

  19. NAND and NOR Implementation • NAND 와 NOR 게이트가 회로적으로 구성 용이함 –어떠한 digital system 이라도 NAND 또는 NOR 로만 구성하는 것이 가능 • NAND Circuit (inverter는 하나의 입력이 ‘1’로 또는 2개의 입력이 하나로 결합된 형태의 NAND로 구현)

  20. NAND and NOR Implementation (NAND : 2-level) • F = ((AB)'(CD)')' = AB + CD • Ex 3-10) Implement the following Boolean function with NAND gates: F(x, y, z) = Σ(1, 2, 3, 4, 5, 7) = xy' + x'y + z

  21. NAND and NOR Implementation(NAND : Multi-level) ‘

  22. NAND and NOR Implementation(NAND) • NAND 의 두가지 표현 방법은? • AND 와 OR 를 NAND 로 나타내시오.

  23. NAND and NOR Implementation(NOR) • NOR Implementation (inverter는 하나의 입력이 ‘0’으로 또는 2개의 입력이 하나로 결합된 형태의 NOR로 구현) • F = (AB' + A'B)(C + D')

  24. NAND and NOR Implementation(NOR) • NOR 의 두가지 표현 방법은? • AND 와 OR 를 NOR 으로 나타내시오. • F = (AB' + A'B)(C + D') 를 NOR 으로 나타내시오.

  25. Wired Logic • Wired AND : Open collector • Wired OR : ECL

  26. 2-LEVEL • AND, OR, NAND, NOR 의 4개의 gate 고려 – 16개의 2 level 가능 • Degenerate form –하나의 동일한 gate 로 표현 가능. 즉 1 level 로 구현 가능 • AND-AND  one AND AND-NAND  one NAND • OR-OR  one OR OR-NOR  one NOR, • NAND-OR  one NAND NAND-NOR  one AND • NOR-AND  one NOR NOR-NAND  one OR • Nondegenerate form • AND-OR, OR-AND : standard form 으로 이미 학습 • NAND-NAND, NOR-NOR : 이미 학습 • NAND-AND, AND-NOR  AND-OR-INVERT 로 구현 • OR-NAND, NOR-OR  OR-AND-INVERT 로 구현 • Example 3-11(a)의 map 을 AND-OR-INVERT로 구현하고, 이를 각각 NAND-AND 및 AND-NOR로 그리시오.

  27. 2-LEVEL (F=(AB+CD+E)’,F=[(A+B)(C+D)E]’)

  28. Exclusive-OR Function • x y = xy' + x'y (만들어볼것) (x y)' = (xy' + x'y)' = xy + x'y' x 0=x x 1=x' x x=0 x x'=1 x y'=x' y=(x y)‘ • A B = B A (A B) C = A (B C) = A B C Fig. 3-32 회로가 EX-OR나오는지 풀어볼 것

  29. Exclusive-OR Function • Parity Generation and Checking P = x y z (송신측) C = x y z P (수신측)

  30. HDL(Hardware Description Language)(퀴즈 및 시험 안 나옴) • VHDL, Verilog HDL • Module Representation //HDL Example 3-1 //Description of the simple circuit of Fig. 3-37 module smpl_circuit(A,B,C,x,y); input A,B,C; output x,y; wire e; and g1(e,A,B); not g2(y, C); or g3(x,e,y); endmodule

  31. HDL(Hardware Description Language) • 다음의 HDL의 내용으로 회로를 그리시오. module smpl_circuit(A,B,C,x,y); input A,B,C; output x,y; wire e; and g1(e,A,B); not g2(y, C); or g3(x,e,y); endmodule

  32. HDL(Hardware Description Language) • Gate Delays - `timescale 1ns/100ps //HDL Example 3-2 //Description of circuit with delay module circuit_with_delay (A,B,C,x,y); input A,B,C; output x,y; wire e; and #(30) g1(e,A,B); or #(20) g3(x,e,y); not #(10) g2(y,C); endmodule

  33. //HDL Example 3-3 //Stimulus for simple circuit module stimcrct; reg A,B,C; wire x,y; circuit_with_delay cwd(A,B,C,x,y); initial begin A = 1'b0; B = 1'b0; C = 1'b0; #100 A = 1'b1; B = 1'b1; C = 1'b1; #100 $finish; end Endmodule module circuit_with_delay (A,B,C,x,y); input A,B,C; output x,y; wire e; and #(30) g1(e,A,B); or #(20) g3(x,e,y); not #(10) g2(y,C); endmodule e

  34. HDL(Hardware Description Language) • Boolean Expressions - AND, OR, NOT => (&), (|), (~) //HDL Example 3-4 // x=A+BC+B’D // y=B’C+BC’D’ //Circuit specified with Boolean equations module circuit_bln (x,y,A,B,C,D); input A,B,C,D; output x,y; assign x = A | (B & C) | (~B & C); assign y = (~B & C) | (B & ~C & ~D); endmodule

  35. HDL(Hardware Description Language) //HDL Example 3-5 //User defined primitive(UDP) primitive crctp (x,A,B,C); output x; input A,B,C; //Truth table for x(A,B,C) = Minterms (0,2,4,6,7) table // A B C : x (Note that this is only a comment) 0 0 0 : 1; 0 0 1 : 0; 0 1 0 : 1; 0 1 1 : 0; 1 0 0 : 1; 1 0 1 : 0; 1 1 0 : 1; 1 1 1 : 1; endtable endprimitive • User-Defined Primitives (UDP) //Instantiate primitive module declare_crctp; reg x,y,z; wire w; crctp (w,x,y,z); endmodule

More Related