Download
1 / 42
420 likes | 433 Vues
Chapter 5. Pipelined Computations. Introduction to Pipelined Computations Computing Platform for Pipelined Computations Example Applications Adding numbers Sorting numbers Prime number generation Systems of linear equations. Introduction to Pipelined Computations.
E N D
Chapter 5 Pipelined Computations • Introduction to Pipelined Computations • Computing Platform for Pipelined Computations • Example Applications • Adding numbers • Sorting numbers • Prime number generation • Systems of linear equations
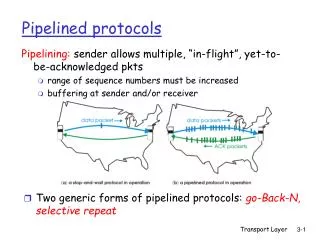
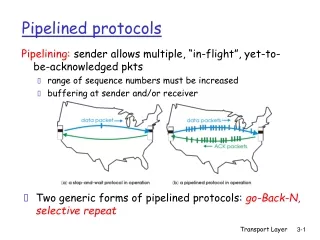
Introduction to Pipelined Computations • We discussed partitioning techniques common to a range of problems in Chapter 4 • We will now discuss a parallel programming technique—pipelining — applicable to a wide range of problems • Pipelining is applicable to problems that are partially sequential in nature • Sequential on the basis of data dependency etc • Can, thus, be used to parallelize sequential code • Problem divided into a series of tasks that have to be completed one after the other • Each task executed by a separate process or processor. • Parallelism viewed as a form of functional decomposition—the functions are performed in succession
Pipelined Computations • Each task/function executed by a separate process or processor. • Imagine what happens in a manufacturing plant • How big/small should a task in each stage of the pipeline be? • What are the trade-offs?
Example 1 • Add all the elements of array ato an accumulating sum: • for (i = 0; i < n; i++) • sum = sum + a[i]; • The loop could be “unfolded” (formulated as a pipeline) to yield • sum = sum + a[0]; • sum = sum + a[1]; • sum = sum + a[2]; • sum = sum + a[3]; • sum = sum + a[4]; • . • . • .
Pipeline for an unfolded loop • The statements are modeled as a chain of producers and consumers • a separate pipeline stage for each statement • Each process viewed as a consumer of data items for the process preceding and as a producer of data for the process following • Each stage accepts the accumulating sum on its input, sin, and one element of the array on its input a, and produces the new accumulating sum on its output, sout
Example 2 • Frequency filter - Objective to remove specific frequencies (f0, f1, f2,f3, etc.) from a digitized signal, f(t). • Signal enters pipeline from left:
Where pipelining can be used to good effect • Assuming problem can be divided into a series of sequential tasks, pipelined approach can provide increased execution speed under the following three types of computations: • If more than one instance of the complete problem is to be executed • 2. If a series of data items must be processed, each requiring multiple operations • 3. If information to start the next process can be passed forward before the process has completed all its internal operations
“Type 1” Pipeline Space-Time Diagram • Assumption: Each process given same time to complete its task • Each time period is one pipeline cycle
“Type 1” Pipeline: Execution Time • With p processes constituting the pipeline and m instances of the problem to execute: • The number of pipeline cycles to execute all instances is • m+p-1 cycles • The average number of cycles is • (m+p-1)/m cycles • tends to one cycle/problem instance for large n • One instance of the problem will be completed in each pipeline cycle after the first p-1 cycles (pipeline latency)
“Type 3” Pipeline Space-Time Diagram • Pipeline processing where information passes to next stage • Utilized in parallel programs where there is only one instance of the problem to execute
Grouping Pipelines • If the number of stages is larger than the number of processors in any pipeline, a group of stages can be assigned to each processor:
Computing Platform for Pipelined Applications • Key requirement: ability to send messages between adjacent processes in the pipeline • Suggests direct communication links • Ideal interconnection structure: multiprocessor system with a line configuration: • Pipelining on clusters requires an interconnection that provides simultaneous transfer between adjacent processors • Most clusters employ a switched interconnection structure that allows such transfers
Example Pipelined Solutions (Examples of each type of computation)
Pipeline Program Examples Adding Numbers Type 1 pipeline computation
Pipeline Example: Adding Numbers (cont’d) Basic code for process Pi : recv(&accumulation, Pi-1); accumulation = accumulation + number; send(&accumulation, Pi+1); except for the first process, P0, which is send(&number, P1); and the last process, Pn-1, which is recv(&number, Pn-2); accumulation = accumulation + number;
SPMD program if (process > 0) { recv(&accumulation, Pi-1); accumulation = accumulation + number; } if (process < n-1) send(&accumulation, P i+1); The final result is in the last process. Instead of addition, other arithmetic operations could be done.
Pipelined addition numbers with a master process and ring configuration
Analysis • Analyses in previous chapters assumed simultaneous computation and communication phases among processes • Many not be appropriate in pipelining because each instance starts at a different time and ends at a different time • Assumption: each process performs similar actions in each pipeline cycle • We’ll then work out the communication and computation required in each pipeline cycle • With a p-stage pipeline and m instances, the total execution time, ttotal, is • The average time for a computation is
Analysis: Single Instance Problem • Consider a case where a single number is being added in each stage, i.e., n=p • The period of one pipeline cycle will be dictated by the time of one addition and one communication: • Each pipeline cycle, tcycle, requires: • With one group of numbers (m=1), the total execution time will take n pipeline cycles and ttotal will be
Analysis: Multiple Instances Problem • With m groups of numbers to add, each resulting in a separate answer, there will be (m+n-1) cycles and ttotal will be: • For large m, the average execution time, ta, is approximately
Data Partitioning with Multiple Instances Problem • Consider the case when each stage processes a group of d numbers • The number of processes is given by p = n/d • Each communication will transfer one result • But the computation will now require d numbers to be accumulated (d-1 steps) plus the incoming number, thus we have: • What is the impact of the size d of data partitioning on performance?
Example 2: Sorting Numbers • A pipeline solution for sorting is to have the first process, P0, accept the series of numbers one at a time, store the largest so far received and pass onward all smaller numbers • Each subsequent process performs the same algorithm, • When no more numbers are to be processed, P0, will have the largest number, P1 the next largest, and so on • The basic algorithm for process Pi, 0<i<p-1,is • recv(&number, Pi-1); • if (number > x) { • send(&x, Pi+1); • x = number; • } else send(&number, Pi+1);
Sorting Numbers A parallel version of insertion sort.
Sorting Numbers (cont’d) • With nnumbers, the ith process will accept n - i numbers • It will pass onward n - i – 1 numbers • Hence, a simple loop could be used. right_procNum = n-i-1; recv(&x, Pi-1); for(j=0; j<right_procNum; j++) recv(&number,Pi-1); if (number > x) { send(&x, Pi+1); x = number; } else send(&number, Pi+1); }
Pipeline for Sorting Using Insertion Sort • A series of operations performed on a series of data items • No opportunity to continue useful work after passing smaller numbers onward Type 2 pipeline computation
Extracting the Sorted Numbers • Results of the sorting algorithm can be extracted from the pipeline using • The ring configuration in Slide 5.19, or • The bi-directional line configuration shown below • Advantage of bi-directional line: process can pass its result as soon as it receives its last input number • More numbers pass thru processes nearer the master
Extracting the Sorted Numbers(cont’d) • Incorporating results being returned, process i, 0<i<p-1, could have the form: right_procNum = n-i-1; recv(&x, Pi-1); for(j=0; j<right_procNum; j++) recv(&number,Pi-1); if (number > x) { send(&x, Pi+1); x = number; } else send(&number, Pi+1); } send(&x, Pi-1); for(j=0; j<right_procNum; j++) recv(&number,Pi+1); send(&number,Pi-1); }
Analysis • Regarding the compare-and-exchange operation as one computational step, the sequential time is: • approximatelyn2/2 number of steps, unsuitable except for very small n. • With n pipeline processes and n numbers to sort, the parallel implementation has • n+n-1 = 2n-1 pipeline cycles. • Each cycle has one compare and exchange operation and one send() • Thus each pipeline requires (See figure on Slide 5.19): • The total execution time is:
Example 3: Prime Number Generation • Sieve of Eratosthenes is a classical way of extracting prime numbers from a series of all integers starting from 2 • First number, 2, is prime and kept. • All multiples of this number are deleted as they cannot be prime. • Process repeated with each remaining number. • The algorithm removes nonprimes, leaving only primes.
Sieve of Eratosthenes: Sequential Code • Sequential program usually employs an array: • with all elements initialized to true and • later reset to false each element whose index is not a prime number for(i=2; i<=n; i++) prime[i] = 1; /* initialize array */ for(i=2; i<=sqrt_n; i++) /* for each prime */ if (prime[i]==1) for(j=i+i; j<=n; j = j+i) prime[j] = 0; /* strike its multiples */
Sieve of Eratosthenes: Sequential Code • There are multiples of 2, multiples of 3 etc. Hence, • Algorithm can be improved so that striking can start at i2 rather than 2i, for a prime i. • Notice that the early terms in the above equation will dominate the overall time • There are more multiples of 2 than 3, more multiples of 3 than 4, etc
Pipelined Sieve of Eratosthenes • A parallel implementation based on partitioning, where each process strikes out multiples of none number will not be effective. Why? • A pipeline implementation can be quite effective: • First a series of consecutive numbers is generated that feeds into the first pipeline stage • This stage extracts all multiples of 2 and passes the other numbers to stage 2 • The second stage extracts all multiples of 3 and passes the other numbers to stage 3 etc
Sieve of Eratosthenes: Parallel Code • The code for a process, Pi, could be based upon recv(&x, Pi-1); /* repeat following for each number */ recv(&number, Pi-1); if ((number % x) != 0) send(&number, P i+1); • Each process will not receive the same amount of numbers and the amount is not known beforehand. • Use a “terminator” message, which is sent at the end of the sequence: recv(&x, Pi-1); for (i = 0; i < n; i++) { recv(&number, Pi-1); if (number == terminator) break; (number % x) != 0) send(&number, P i+1); }
Example 4: Solving a System of Linear Equations • The final example is Type 3, where a process can continue with useful work after passing on information • This is demonstrated by solving a system of linear equations of upper-triangular form: • We need to for x0,x1, …, xn-1, where the a’s and the b’s are constants.
Back Substitution • First, the unknown x0 is found from the last equation; i.e., • Value obtained for x0 substituted into next equation to obtain x1; i.e., • Values obtained for x1 and x0 substituted into next equation to obtain x2: and so on until all the unknowns are found.
Pipeline Solution • This algorithm can be implemented as a pipeline: • First pipeline stage computes x0 and passes x0 onto the second stage, • The second stage computes x1 from x0 and passes both x0 and x1 onto the third stage, • The third stage computes x2 from x0 and x1, and so on. Type 3 pipeline computation
Pipeline Solution (cont’d) • Each pipeline stage can be implemented with one process • There are p=n processes for n equations • The ith process (0 < i < p) receives the values • x0, x1, x2, …, xi-1 • and computes xi from the equation:
Sequential Code • Given the constants ai,jand bkstored in arrays a[][]and b[], respectively, and the values for unknowns to be stored in an array, x[], the sequential code could be x[0] = b[0]/a[0][0]; /* computed separately */ for (i = 1; i < n; i++) { /*for remaining unknowns*/ sum = 0; for (j = 0; j < i; j++ sum = sum + a[i][j]*x[j]; x[i] = (b[i] - sum)/a[i][i]; }
Parallel Code • Pseudocode of process Pi (i < p-1) of could be sum = 0; for (j = 0; j < i; j++) { recv(&x[j], Pi-1); send(&x[j], Pi+1); sum = sum + a[i][j]*x[j]; } x[i] = (b[i] - sum)/a[i][i]; send(&x[i], Pi+1); • Now we have additional computations to do after receiving and resending values.
