1 / 18

Solutions to group problems

This text discusses the characteristics of jump chains in stochastic processes, focusing on their transition probabilities. It explores the relationships between the states in the chain, emphasizing the concepts of absorbing states and stationary distributions. An example of a 0-1 process with a transition matrix that has a stationary distribution of (1/2, 1/2) is considered, highlighting the importance of understanding these systems in probability theory and statistical mechanics.

gerry
Télécharger la présentation

Solutions to group problems

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

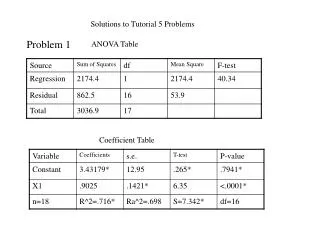
    1. Solutions to group problems gi,i-1=i? gii=-i(???) gi,i+1=i? Hence -gi,i+1/gii=???????=1-(-gi,i-1/gii). Thus the jump chain goes up one step with probability ????????and down one step with probability ?????????0 is an absorbing state. 2. Consider a 0-1 process. It has jump chain with transition matrix and stationary distribution (1/2,1/2), but the stationary distribution of the process itself is

More Related