1 / 18

Understanding Mass Balance and Transport Mechanisms in Thermodynamic Systems

This article explores the principles of mass balance and mass flow in thermodynamic systems, including both diffusion and convection processes. We discuss the equations governing mass transport through permeable membranes, equilibrium conditions, and how alterations in pressure and temperature affect species activity. The concepts of momentum and energy balance are also highlighted, illustrating their significance in natural phenomena and engineered systems. This comprehensive overview helps grasp the underlying dynamics of mass transport and equilibrium in various phases.

hall-cobb
Télécharger la présentation

Understanding Mass Balance and Transport Mechanisms in Thermodynamic Systems

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

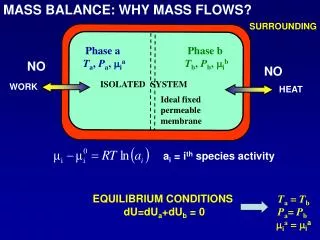
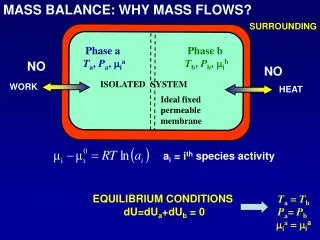
  1. MASS BALANCE: WHY MASS FLOWS? SURROUNDING Phase a Ta, Pa, mia Phase b Tb, Pb, mib NO NO ISOLATED SYSTEM WORK HEAT Ideal fixed permeable membrane ai = ith species activity Ta = TbPa= Pb mia = mia EQUILIBRIUM CONDITIONS dU=dUa+dUb = 0

  2. MASS BALANCE: EQ.CON. ALTERATION 1 Pa increase (>Pb) [Ta = Tb; mia = mib] Phase a T, Pa, mi Phase b T, Pb, mi MASS TRASPORT (CONVECTION) permeable membrane

  3. mia>mib [Ta = Tb; Pa = Pb] 2 Phase a T, P, mia Phase b T, P, mib permeable membrane MASS TRASPORT (DIFFUSION) Mass transport represents a possible way the system has to get new equilibrium conditions once the original ones have been altered.

  4. MASS BALANCE Z X Y DZ DX (X+DX, Y+ DY, Z+ DZ) G (X, Y, Z) DY (X, Y+ DY, Z) (X+DX, Y+ DY, Z)

  5. MASS BALANCE: EXPRESSION DX DZ (X, Y, Z) G DY Ci = f(X, Y, Z, t)

  6. DX DZ (X, Y, Z) G DY DIVIDING FOR DV

  7. FLUXES EXPRESSIONS Ideal solution Diffusion Diffusion Diffusion Convection Convection Convection Bi = mobility of the diffusing components

  8. Remembering that:

  9. MASS BALANCE EQUATION FOR ith SPECIES where: Remembering the definition of the NABLA operator:

  10. As: … the summation of ith mass balance over all the r components yields to the well known continuity equation:

  11. MASS BALANCE: CYLINDRICAL COORDINATES Jir+dr Jir+dr Jiz Jiz+dz Jir Jir Jir Jiz Jiz+dz Jir+dr r dr dz TWO DIMENSIONS r z

  12. Ci = f(z, r, t) r dr dz Dividing by 2prdrdz

  13. Constant diffusion coefficient D Remembering the derivativedefinition

  14. MOMENTUM BALANCE Incoming sand Escaping sand Sand containing vessel Sliding vessel motion direction Inclinate plane Friction Gravity NO Yes

  15. DZ DX (X+DX, Y+ DY, Z+ DZ) (X, Y, Z) DY (X, Y+ DY, Z) (X+DX, Y+ DY, Z) Body forces: gravitational, electro-magnetic fields Surface forces: viscous drag and pressure

  16. Surface forces gravitational field Incoming and exiting mass

  17. ENERGY BALANCE Conduction Expansion Viscous heating

More Related