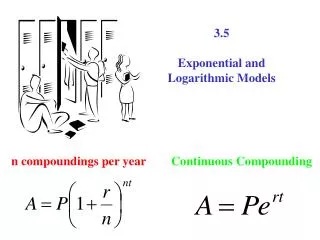
4.8 Exponential and Logarithmic Models
110 likes | 452 Vues
4.8 Exponential and Logarithmic Models. Exploring - 3 Exponential Models. Uninhibited Growth/Decay. Newton’s Law of Cooling Temperature decreases exponentially over time. Exponential growth/decay with limiting factors Logistic Model. Examples of growth/decay models.

4.8 Exponential and Logarithmic Models
E N D
Presentation Transcript
Exploring - 3 Exponential Models Uninhibited Growth/Decay • Newton’s Law of Cooling • Temperature decreases exponentially over time • Exponential growth/decay with limiting factors • Logistic Model
Examples of growth/decay models • Examples which demonstrate the growthmodel: • Populations of people • Populations of organisms (cells, bacteria, …) • Examples which demonstrate the decay model: • Radioactive decay • Carbon 14 dating
Exponential Growth and Decay The amount A of an object present at time t is given by where A0 is the original amount of the object and k is the rate of decay or growth (k > 0 if growth and k < 0 if decay) k > 0 k < 0
Uninhibited Growth Model Example 1: A colony of bacteria grows according to the law of uninhibited growth. If 100 grams of bacteria are present initially, and 250 grams are present after two hours, how many will be present after 4 hours?
Uninhibited Decay Model (Half-Life) Example 2: The half-life of Uranium-234 is 200,000 years. If 50 grams of Uranium-234 are present now, how much will be present in 1000 years (Half-life is the time required for half of a radioactive substance to decay).
Newton’s Law of Cooling The temperature u of a heated object at time t is : where T is constant temperature of surrounding medium, is the initial temperature of the object, and k < 0 Example 3: A thermometer at 8 C is brought into a room with constant temperature 35 C. If the thermometer reads 15 C after 3 minutes, what will it read after 5 minutes?
Logistic Growth and Decay Models In logistic models, the population P after time t obeys where a, b, and c are constants with c > 0, and c represents the carrying capacity. b < 0 b > 0
Logistic Growth The logistic growth model represents the amount of bacteria (in grams) after t days 1) Graph the function using a graphing utility. 2) What is the carrying capacity? 3) What was the initial amount of bacteria?
Logistic Growth The logistic growth model represents the amount of bacteria (in grams) after t days 4) When will the amount of bacteria be 300 grams?
Homework p. 334, #1, 3, 6, 7, 16, 23, 24e, 30d 4.8 Exponential and Logarithmic Models