1 / 17

Valuation of Concepts Using Conjugate Möbius Function: Hierarchies and Diversity Analysis

This study explores the valuation of concepts through the Conjugate Möbius Function (CMI), focusing on context and concept lattices. It examines the hierarchical structure of concepts, emphasizing their diversity and weights in relation to attributes like skills in team-building scenarios. By utilizing incidence matrices, the framework assigns values to concepts, facilitating a better understanding of dissimilarity and compact team formation. This research paves the way for future studies on optimizing skill coverage and enhancing team effectiveness based on conceptual analysis.

honey
Télécharger la présentation

Valuation of Concepts Using Conjugate Möbius Function: Hierarchies and Diversity Analysis

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Concepts Valuation by Conjugate Möebius Function • Background • Context, Concept and Concept Lattice • Diversity Function • Conjugate Möebius Inverse • Concept Lattice Valuation • Diversity, Weight, CMI • Dissimilarity, hierarchy • Splitting into hierarchy • Basic interpretation of numbers • Conclusion • Next research • References

  2. Context, Concept and Concept Lattice • Context • Incidence matrix Description of objects and features in incidence matrix. C = cat q = quadrupped (four feet) M = monkey (chimpanzee) p = pilli D = dog i = intelligence F = fish (delphinus) w = live in water H = human h = hand W = whale Whales live in water

  3. Context, Conceptand Concept Lattice • Concept Sample of formal concept:({C,M,D},{p})

  4. Context, Concept and Concept Lattice • Concept lattice

  5. Concept Lattice Valuation • Diversity

  6. Concept Lattice Valuation • CMI

  7. Concept Lattice Valuation

  8. Concept Lattice Valuation • Weighting by CMI

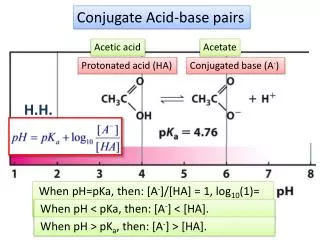
  9. Concept Lattice Valuation • Dissimilarity There are two models in Theory of Diversity. Hierarchical a more generalline model. Concept lattice are hierarchical ordered. But, weighting of concepts is a difficult task. We can assign value to concepts only in small simly lattice because of next condition.

  10. Concept Lattice Valuation

  11. Concept Lattice Valuation • Splitting into hierarchies

  12. Splitting into hierarchies

  13. Basic interpretation of numbers • What represent the numbers (diversity, weight) • For example, we have a set of different people with different skills. We are looking for teams of people (concepts), which can cover most of required skills. • 1. We assign value to each attribute. Higher value represents more important attribute. • 2. We compute diversities of concepts = v(Ci). • 3. v(Ci) / v(Ctop) … upon normalization we get a number that represents measure of covering of skills according to their values. • We want to find „compact“ teams (concepts) whose members have general knowledge. Compact = most of skills of pleople in the team are shared. • 1. We assign value to each attribute. Higher value represents more important attribute • 2. We compute diversities and weights of concepts = v(Ci), (Ci) • 3. v(Ci) / v(Ctop) … upon normalization we get a number that represents measure of covering of skills according to their values. • 4. (Ci) / (v(Ci) / v(Ctop))

  14. Basic interpretation of numbers

  15. Basic interpretation of numbers

  16. Conclusion • Next research • Input • Output • Evaluated, reduced concept lattice Hierarchy of attributes Incidence matrix

  17. Conclusion

More Related