1 / 4

Understanding Venn Diagrams: Probabilities of Events in Different Scenarios

This text explains the use of Venn diagrams to illustrate probabilities involving multiple events. It presents various scenarios such as owning items (cars, air conditioners), academic subjects (history, math), and judicial outcomes (jury and judge convictions). Through specific examples and calculations, the text breaks down the relationships between events, demonstrating concepts like union, intersection, and the complement of events. The probabilities derived offer insights into how overlapping categories influence decision-making and statistical interpretation.

kaveri
Télécharger la présentation

Understanding Venn Diagrams: Probabilities of Events in Different Scenarios

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

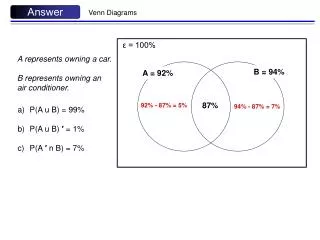
  1. Answer Venn Diagrams ε = 100% A represents owning a car. B represents owning an air conditioner. B = 94% A = 92% 87% 92% - 87% = 5% 94% - 87% = 7% • P(A u B) = 99% • P(A u B) ′ = 1% • P(A ′ n B) = 7%

  2. Answer Venn Diagrams ε = 100% H represents history. M represents maths. M = 50% H = 35% 35%+ 50% - 70% = 15% 35% - 15% = 20% 50% - 15% = 35% 100% - 30% = 70% H′nM′ = 30% • P(H u M) = 100% - 30% = 70% • Use P(H u M) = P(H) + P(M) – P(H n M)P(H n M) = 35% + 50% - 70% = 15% • P( only one of the subjects) = ( P(H) – P(H n M) ) + ( P(M) – P(H n M) ) • = ( 35% - 15% ) + ( 50% - 15% ) = 55%

  3. Answer Venn Diagrams ε = 1 A = first light red B = second light red B = 0.6 A = 0.7 0.4 0.7 – 0.4 = 0.3 0.6 – 0.4 = 0.2 • P(A u B) = 0.9 • P(A u B)’ = 0.1 • P(A’ n B) = 0.2

  4. Answer Venn Diagrams ε = 100% A = jury convicts B = judge convicts B = 73% A = 67% • P(A n B′) = 67% - 46% = 21% • P(A′ n B) = 73% - 46% = 27% • P(A n B′) + P(A′ n B) = 21% + 27%= 48% • 100% – (A u B) (A u B) = (A) + (B) – ( A n B ) • = 67% + 73% – 46% • = 94% • The percentage neither the panel nor the judge would convict = 100% – 94% = 6% 46% 67% - 46% = 21% 73% - 46% = 27% 67% + 73% – 46% = 94% 100% - 94% = 6%

More Related