Řešení rovnic
230 likes | 683 Vues
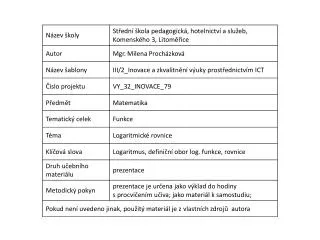
Řešení rovnic. Iracionální rovnice. Autorem materiálu a všech jeho částí, není-li uvedeno jinak, je Ing. Šárka Macháňová. Dostupné z Metodického portálu www.rvp.cz, ISSN: 1802-4785, financovaného z ESF a státního rozpočtu ČR.

Řešení rovnic
E N D
Presentation Transcript
Řešení rovnic Iracionální rovnice • Autorem materiálu a všech jeho částí, není-li uvedeno jinak, jeIng. Šárka Macháňová. • Dostupné z Metodického portálu www.rvp.cz, ISSN: 1802-4785, financovaného z ESF a státního rozpočtu ČR. • Provozuje Národní ústav pro vzdělávání, školské poradenské zařízení a zařízení pro další vzdělávání • pedagogických pracovníků.
Iracionální rovnice Iracionální rovnice jsou rovnice, které obsahují odmocniny z neznámé nebo z výrazů s neznámou. Příklady takových rovnic:
Řešení iracionálních rovnic ‒ důsledková úprava Iracionální rovnice zpravidla řešíme v oboru reálných čísel a stěžejním krokem je umocnění rovnice. Umocnění není ekvivalentní úpravou, ale úpravou tzv. důsledkovou. Jaké „důsledky“ může mít použití důsledkové úpravy? Podívejme se na dvě zajímavá umocnění, jedné rovnosti a jedné nerovnosti: Po umocnění, to najednou vypadá na dvě rovnosti. Je to v pořádku? Ano. Z čísel, která se nerovnala, jsme najednou získali čísla, která se rovnají. I přesto, že tedy nejde o ekvivalentní úpravu, budeme umocňování používat. Jinak to nejde. Ale… Protože jsme z nerovnajících se čísel dostali čísla, která se rovnají, může se objevit i při řešení iracionálních rovnic něco, co se bude tvářit jako výsledek, ale výsledek to nebude (z umocňování nerovnosti 5 ‒5 je vidět, odkud takový falešné výsledky vzejde). Abychom takové falešné výsledky „odbourali“, budeme muset vždy dělat zkoušku (vyzkoušet všechny „výsledky“, zda jsou pravé či falešné).
Řešení iracionálních rovnic ‒ důsledková úprava Umocňování je tedy důsledková úprava. Při použití důsledkové úpravy neztratíme žádné správné řešení, ale mohou se objevit klamná další řešení. Proto vždy provádíme zkoušku. Pojďme si tedy vše ukázat v praxi na konkrétním příkladu. Řešme v R rovnici: Nejdříve určíme definiční obor, který plyne z toho, že výraz pod druhou odmocninou musí být nezáporný!
Řešení iracionálních rovnic ‒ důsledková úprava Umocňování je tedy důsledková úprava. Při použití důsledkové úpravy neztratíme žádné správné řešení, ale mohou se objevit klamná další řešení. Proto typicky provádíme zkoušku. Pojďme si tedy vše ukázat v praxi na konkrétním příkladu. Řešme v R rovnici: No a nyní již pojďme rovnici řešit. Hned na úvod použijeme právě probranou důsledkovou úpravu umocnění rovnice.
Řešení iracionálních rovnic ‒ důsledková úprava Umocňování je tedy důsledková úprava. Při použití důsledkové úpravy neztratíme žádné správné řešení, ale mohou se objevit klamná další řešení. Proto typicky provádíme zkoušku. Pojďme si ti tedy vše ukázat v praxi na konkrétním příkladu. Řešme v R rovnici: No a nyní tedy musíme zkouškou zkontrolovat, zda některé řešení není klamné.
Řešení iracionálních rovnic ‒ důsledková úprava Řešme v R rovnici: Zkouška: Zkouška vyšla ⇒ x = 7 je řešením rovnice. Zkouška nevyšla ⇒ x = 2 není řešením rovnice (zároveň je vidět, že po umocnění rovnice by se její strany začaly rovnat). Rovnice má jediné řešení x = 7. Píšeme:
Řešení iracionálních rovnic ‒ důsledková úprava Tak ještě jednou pěkně po pořádku. Řešme v R rovnici: Nejdříve určíme definiční obor, který plyne z toho, že výrazy pod druhými odmocninami musí být nezáporné!
Řešení iracionálních rovnic ‒ důsledková úprava Tak ještě jednou pěkně po pořádku. Řešme v R rovnici: A nyní již začneme řešit rovnici.
Řešení iracionálních rovnic ‒ důsledková úprava Tak ještě jednou pěkně po pořádku. Řešme v R rovnici:
Řešení iracionálních rovnic ‒ důsledková úprava Řešme v R rovnici: No a nyní musíme zkouškou zkontrolovat, zda některé řešení není klamné. Zkouška: Zkouška vyšla ⇒ x = 10 je řešením rovnice. Zkouška nevyšla ⇒ x = 362 není řešením rovnice. Rovnice má jediné řešení x = 10. Píšeme:
Příklady k procvičení Vyřeš v R rovnici:
Příklady k procvičení Vyřeš v R rovnici: Určíme definiční obor: Vyřešíme rovnici: Zkouška: Zkouška vyšla ⇒ x = 25 je řešením rovnice.
Příklady k procvičení Vyřeš v R rovnici:
Příklady k procvičení Vyřeš v R rovnici: Určíme definiční obor: Vyřešíme rovnici:
Příklady k procvičení Vyřeš v R rovnici: Zkouška: Zkouška vyšla ⇒ x = 4 je řešením rovnice. Zkouška vyšla ⇒ x = ‒5 je řešením rovnice.
Příklady k procvičení Vyřeš v R rovnici:
Příklady k procvičení Vyřeš v R rovnici: Určíme definiční obor: Vyřešíme rovnici:
Příklady k procvičení Vyřeš v R rovnici: Vyřešíme rovnici:
Příklady k procvičení Vyřeš v R rovnici: Uděláme zkoušku: Zkouška vyšla ⇒ x = 2 je řešením rovnice. Zkouška vyšla ⇒ x = ‒14/9 je řešením rovnice.
Příklady k procvičení Vyřeš v R rovnici:
Příklady k procvičení Vyřeš v R rovnici: Určíme definiční obor: Vyřešíme rovnici: Uděláme zkoušku: Zkouška vyšla ⇒ x = 1, 2 je řešením rovnice.
Použité obrázky: Všechny uveřejněné odkazy [cit. 2010-06-10]. Dostupné pod licencí Public domain na WWW: <http://www.clker.com/clipart-white-board.html>