1 / 130

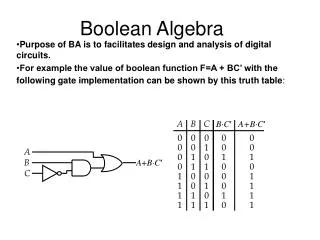
Boolean Algebra

Boolean Algebra. Starter Task. State 5 basic data types together with one operation that can be performed on each . We have looked at 4 in the past few weeks... . Answers. Variable Array Insert a value into a certain position in the array Stack Pop, Push Queue enQueue , Serve

lisbet
Télécharger la présentation

Boolean Algebra

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Boolean Algebra

  2. Starter Task • State 5 basic data types together with one operation that can be performed on each. • We have looked at 4 in the past few weeks...

  3. Answers • Variable • Array • Insert a value into a certain position in the array • Stack • Pop, Push • Queue • enQueue, Serve • Binary Tree • Search through and add values / Delete values • Linked List • Add items to the list, remove items from the list

  4. Over the next Few Weeks... • Working through the booklets... • Binary Numbers • Hexadecimal Numbers • Characters • ASCII – Strings and Character sets • Negative Numbers • Two’s complement, representation sign, magnitude • Shifting • Fixed Point, Floating Point • Conversion + Benefits • Rounding + Truncation effects on accuracy • Overflow, Underflow

  5. We use Base 10... • Because we have 10 fingers

  6. What if we had 16?

  7. This gives us the structure of... • Every 10th value we add an extra number... • 2 • 12 • 23 • 178 • Etc...

  8. Base 10 looks like... • The number 1583 means 1 'thousand', 5 'hundreds', 8 'tens' and 3 'units'...

  9. Where each column is 10^X • 10^1 = 10 • 10^2 = 100 • 10^3 = 1000 • 10^4 = 10,000

  10. Consider this... • Computers only use base 2... • How would this look in a table? • What will a base 2 set of numbers look like?

  11. Base 2

  12. Base 2

  13. Representing numbers... • What number do you think this will represent? • 10010110

  14. Base 2

  15. 150

  16. What do the following numbers = • 10000101 • 01000001 • 11111111 • 10110101 • 00000000 • 10101111 • 00101010 • 00111011 • 10111010

  17. Answers • 10000101 = 128 + 0 + 0 + 0 + 0 + 4 + 0 + 1 = 133 • 65 • 255 • 181 • 0 • 175 • 42 • 59 • 186

  18. What if I wanted to go the other way... • How would I convert 22 into binary?

  19. Actions • 22 / 2 = 11 r 0 • _ _ _ _0

  20. Actions • 22 / 2 = 11 r 0 • 11 / 2 = 5 r 1 • _ _ _10

  21. Actions • 22 / 2 = 11 r 0 • 11 / 2 = 5 r 1 • 5 / 2 = 2 r 1 • _ _110

  22. Actions • 22 / 2 = 11 r 0 • 11 / 2 = 5 r 1 • 5 / 2 = 2 r 1 • 2 / 2 = 1 r 0 • _ 0110

  23. Actions • 22 / 2 = 11 r 0 • 11 / 2 = 5 r 1 • 5 / 2 = 2 r 1 • 2 / 2 = 1 r 0 • 1 / 2 = 0 R 1 • 1 0110

  24. What if I wanted to go the other way... • How would I convert 22 into binary?

  25. Actions • Divide each value into largest number and put a one in the table...

  26. What are the following binary numbers? • 156 • 45 • 78 • 97 • 123 • 245 • 253 • 7 • 184 • 111

  27. What are the following binary numbers? • 156 = 10011100 • 45 = 00101101 • 78 = 01001110 • 97 = 01100001 • 123 = 01111011 • 245 = 11110101 • 253 = 11111101 • 7 = 00000111 • 184 = 10111000 • 111 = 01101111

  28. Bytes • So far everything has consisted of once byte... • 8 bits... Byte • 4bits... Nybble (rarely used now) • 1101=13

  29. Standard Computers are 32bit... • What would be the maximum value that a 32bit computer can hold? • You might want to use a calculator...

  30. 32 bit = 4,294,967,295 • This is the biggest value for a 32bit computer... • However it doesn’t exist in many operating systems...

  31. 64Bit... • What about 64bit?

  32. Again... • 18,446,744,073,709,552,000 • This number will not be found in 64bit operating systems... • Can you look down the list of contents in the booklet to see why?

  33. Summary Video’s • http://www.youtube.com/watch?v=qdFmSlFojIw • http://courses.cs.vt.edu/csonline/NumberSystems/Lessons/DecimalToBinaryConversion/index.html

  34. Convertor • http://mistupid.com/computers/binaryconv.htm

  35. Lesson 2 • Hexadecimal notation... • What do you think hexadecimal notation looks like?

  36. Hexadecimal notation

  37. What’s it used for • Give a more readable notation for people to use. • Decimal = 10,995 • Binary = 10101011110011 • Hexadecimal = 2AF3 

  38. How it’s used... • Have you ever seen... • #33FD56 • In HTML coding... • Gives you a colour • #33FD56

  39. Each part = nybble • #33FD56 • 33 = 51 =0011 0011 • FD = 253 =1111 1101 • 56 = 86 =0101 0110

  40. Task 2 • Fill in the table: You will have to remember how to complete binary numbers...

  41. Now we have 3 ways to represent numbers... • What is the point? • We can represent 0-255 numbers using 1byte or 1 hexadecimal code • Can you think of why we would use this?

  42. Character Sets • All the symbols, letters, numbers have a binary representation • There are 128 different characters that we call ASCII This is a Standard!

  43. ASCII • (American Standardised Code for Information Interchange) • Needed so that computers share documents together: Others include: EBCDIC(Extended Binary Coded Decimal Interchange Code) ISO 8859, for ß (German), ñ (Spanish), å (Swedish) ANSI (American National Standards Institute)

  44. ASCII Character Set

  45. Words • In order to write the word Hello

  46. Task • How would hello world read? • How many bits are used for each character?

  47. Hello World • 01001000 01100101 01101100 01101100 01101111 00100000 01010111 01101111 01110010 01101100 01100100

  48. Hello World • 48 65 6c 6c 6f 20 57 6f 72 6c 64

  49. Practice • What about the sentence: • There are 10 types of people in the world: those who understand binary, and those who don't. 

More Related