Download
1 / 10
100 likes | 228 Vues
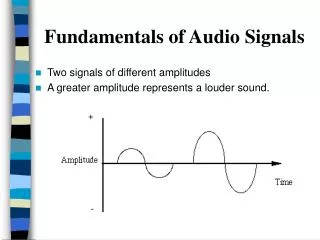
In today's lecture on Signal Processing, we explore concepts such as error signals, convergence of Fourier synthesis, and frequency modulation, particularly focusing on chirp signals. We discuss how waveforms can be synthesized using the equation x(t) = A0 + ∑Ak.cos(2πfkt + φk), where amplitudes, phases, and frequencies may vary. The lecture highlights how real-world signals, like music, exhibit frequency changes over time, exemplified by the linear frequency shift seen in chirp signals. We also present synthesis techniques for generating frequency sweeps.
E N D
Signals & Systems Lecture 17: Chapter 3 Spectrum Representation
Today's lecture • Error signal • Convergence of Fourier synthesis • Frequency modulation • Chirp formula
Convergence of Fourier Synthesis • Error Signal: • Worst-case error:
General Waveforms • Waveforms can be synthesized by the equation x(t) = A0 + ∑Ak cos(2πfkt +k) • These waveforms maybe • constants • cosine signals ( periodic) • complicated-looking signals (not periodic) • So far we have dealt with signals whose amplitudes, phases and frequencies do not change with time
Frequency Modulation • Most real-world signals exhibit frequency change over time e.g. music. • Frequency of a signal may change linearly with time which sounds like a siren or chirp • Chirp signal: Signal whose frequency changes linearly with time from some low value to high value • Let x(t) =Acos(ω0t + ) =Acosψ(t) ψ(t) = ω0t + and dψ(t)/dt = ω0 whereψ(t) denotes the time varying angle function
Frequency Modulation • We can create a signal with quadratic angle function by defining ψ(t) = 2πμt2 + 2πf0t + • instantaneous frequency = slope of the angle function ωi= dψ(t)/dt fi(t) = 1/2 π dψ(t)/dt fi(t) = 2μt + f0
Example 3.8: Synthesize a Chirp Formula Synthesize a frequency sweep from f1 = 220 Hz to f2 = 2320 Hz over a 3-second time interval. fi(t) = (f2 -f1)t / T2 + f1 ψi(t) = ∫ ωi(u) du t 0
