1 / 8

Constructions

Constructions. Mathematical Drawings using a Compass and Straight Edge. For A.S 1.4 Use Geometric Techniques to produce a pattern or object. Internal, 2 Credits. Hexagon. Perp. Bisector. Angle Bisector. Perp. Pt on line. Perp. Pt off line. Parallel Line.

merrill
Télécharger la présentation

Constructions

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Constructions Mathematical Drawings using a Compass and Straight Edge. For A.S 1.4 Use Geometric Techniques to produce a pattern or object. Internal, 2 Credits Hexagon Perp. Bisector Angle Bisector Perp. Pt on line Perp. Pt off line Parallel Line

  2. Constructing a hexagon:eg.construct a hexagon with 6cm sides (click once to start) 1. Set your compass to the required side length (6cm in this case) 2. Construct a circle using this radius. 3. Starting anywhere on the circumference, “walk” your compass around the circumference, scribing arcs as you go. 4. Join up all your arc crossings. You now have a regular hexagon with 6 cm sides. 6 cm 6 cm Hexagon Perp. Bisector Angle Bisector Perp. Pt on line Perp. Pt off line Parallel Line

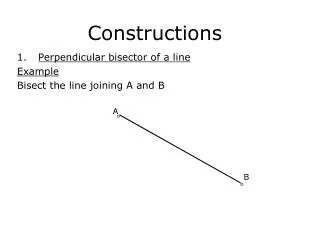
  3. Perpendicular Bisector or MediatorTo Bisect Line AB: (click once to start) 1. With Compass point on A, scribe the blue arcs. 2. With Compass on B scribe the green arcs. 3. Join the arc crossings to show the mediator. NB: Point C is called the “Midpoint” of line AB B C A Hexagon Perp. Bisector Angle Bisector Perp. Pt on line Perp. Pt off line Parallel Line

  4. Angle Bisector (click once to start) • Make two arcs (same radius) from B which cut AB at D and BC at E. • Make two arcs (same radius) from D and E – which meet at arc crossing, F. A F • Join FB. C D E B Hexagon Perp. Bisector Angle Bisector Perp. Pt on line Perp. Pt off line Parallel Line

  5. Perpendicular through a Point on the line: (click once to start) • Make two arcs (same radius) from C which cut AB at D and E. (Extend AB if necessary). • Setting compass to a larger radius, make arcs from D and E, crossing at F. • Join FC. F B E C A D Hexagon Perp. Bisector Angle Bisector Perp. Pt on line Perp. Pt off line Parallel Line

  6. Perpendicular through a Point **NOT** on the line: (click once to start) • Make two arcs (same radius) from C which cut AB at D and E. (Extend AB if necessary). • Setting compass to a larger radius, make arcs from D and E, crossing at F. • Join FC. F B E D A C Hexagon Perp. Bisector Angle Bisector Perp. Pt on line Perp. Pt off line Parallel Line

  7. A line parallel to, and a certain distance from a line: (click once to start) Eg. construct the line 2cm above line AB. • Set the compass to the distance required – 2cm in this case. • Make a number of arcs (same radius) from line AB. (ie with the point of the compass at random points on the line) • Rule a line over the top of the “waves”. B 2 cm A Hexagon Perp. Bisector Angle Bisector Perp. Pt on line Perp. Pt off line Parallel Line

  8. end Hexagon Perp. Bisector Angle Bisector Perp. Pt on line Perp. Pt off line Parallel Line

More Related