1 / 7

Mergesort

Mergesort. Inhalt. 1. Geschichtliches 2. Funktionsweise 3.Beispiel 4.Komplexität. Geschichte. 1945 Von John von Neuermann vorgestellt Er heißt Mergesort (Merge = Mischen) Weil bei Ihm im Gegensatz zu anderen Sortieralgorithmen der Schwerpunkt im Mischen und nicht im Aufteilen liegt.

mikel
Télécharger la présentation

Mergesort

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Mergesort

  2. Inhalt • 1. Geschichtliches • 2. Funktionsweise • 3.Beispiel • 4.Komplexität

  3. Geschichte • 1945 Von John von Neuermann vorgestellt • Er heißt Mergesort (Merge = Mischen) Weil bei Ihm im Gegensatz zu anderen Sortieralgorithmen der Schwerpunkt im Mischen und nicht im Aufteilen liegt. • Er wird Rekursiv verwendet.

  4. Funktionsweise • Die grundlegende Funktionsweise ist das zerteilen einer Gruppe in Untergruppen und das sortieren der Untergruppen. • Sollten die Untergruppen dennoch Zu gros sein werden sie wiederum je In zwei Hälften geteilt. • Daher wird dieser Algorithmus Rekursiv verwendet.

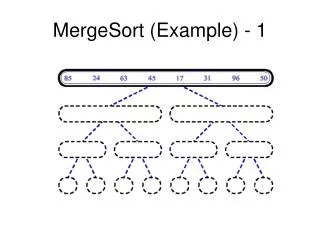
  5. Beispiel • Gegeben ist eine Buchstabenreihenfolge: duasfjnlsefk die alphabetisch geordnet werden soll. Als erstes wird nach dem Mergeverfahren die Gruppen in zwei Hälften geteilt dazu nimmt man einfachshalber die linke und die rechte Hälfte. duasfjnlsefk Dieser Schritt wird nun öfters wiederholt: duasfjnlsefk d ua s fj n ls e fk d u a s f j n l s e f k Bis man nur noch einzelne Elemente hat.

  6. Beispiel • Nun kommt der Hauptteil des Mergesort das richtige zusammensetzen dabei macht man die Zersetzungsschritte Rückgängig und ordnet dabei die Buchstaben. d u a s f j n l s e f k d au s fj n ls e fk adu fjs lns efk adfjsu efklns adeffjklnssu duasfjnlsefk  adeffjklnssu

  7. Komplexität • Seine Komplexität (Worst-, Best- und Average-Case-Verhalten) beträgt stets O(n * log(n)) • Somit ist Mergesort ein stabiler Algorithmus.

More Related