1 / 25

Coordinate Transfer needs

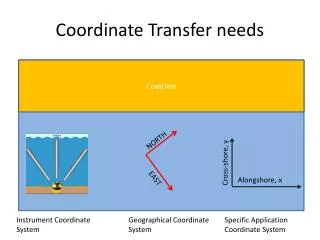
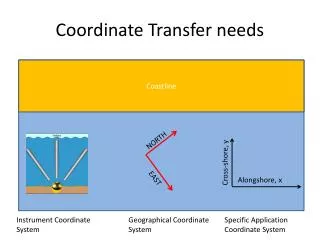
Coordinate Transfer needs. Coastline. NORTH. Cross-shore, y. Alongshore, x. EAST. Instrument Coordinate System. Geographical Coordinate System. Specific Application Coordinate System. Rotation Matrix. (1) Rotation of the axes. (2) Rotation of an Object relative to fixed axes. x.

mimi
Télécharger la présentation

Coordinate Transfer needs

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Coordinate Transfer needs Coastline NORTH Cross-shore, y Alongshore, x EAST Instrument Coordinate System Geographical Coordinate System Specific Application Coordinate System

  2. Rotation Matrix • (1) Rotation of the axes. • (2) Rotation of an Object relative to fixed axes x yo θ xo y

  3. Rotate Co-ordinate Axis System(anti-clockwise) y y yo ѳ xo x x

  4. Rotate Object (anti-clockwise)= Rotate Axis (clockwise) y y y1 x1 ѳ x x

  5. Rotate Co-ordinate Axis System y y yo y’ xo x x ѳ ѳ x’

  6. square = 0 0 0 1 1 1 1 0 0 0 Sq2 = 0 0 0.3420 0.9397 1.2817 0.5977 0.9397 -0.3420 0 0 theta = 20 Sq1 = 0 0 -0.3420 0.9397 0.5977 1.2817 0.9397 0.3420 0 0

  7. Example • (1) Make a matlab script that does the rotation (2-d) • (2) Make it a function • (3) Rotate some current data

  8. function X1=rotate_2d(X,a) • % • [m,n]=size(X); • j=1; • if n==2; • X=X'; • j=2; • end • R=[ cos(a) sin(a) • -sin(a) cos(a) ]; • X1=R*X; • if j==2; • X1=X1'; • end • end

  9. a=load('Springmaid_Dec_2005.txt'); yyyy = a(:,1); mo = a(:,2); dd = a(:,3); hh = a(:,4); mi = a(:,5); ss = a(:,5); % u = a(:,7); v = a(:,8); % Time = datenum(yyyy,mo,dd,hh,mi,ss); % U=[u,v]; Uxy=rotate_2d(U,45); ux = Uxy(:,1); uy = Uxy(:,2); % figure subplot(211); plot(Time,u,Time,v); legend('u','v') subplot(212); plot(Time,ux,Time,uy); legend('along','cross') % figure subplot(211); quiver(Time-Time(1),Time*0,u,v); axis equal subplot(212); quiver(Time-Time(1),Time*0,ux,uy); axis equal

  10. Rotations around x-, y- and z- axes • Pitch is up and down like a box lid. • Yaw is left and right like a door on hinges (Heading) • Roll is rotation.

  11. Anticlockwise rotations around x-, y- and z- axes z Roll y α z β Pitch x γ y Yaw x Anticlockwise rotations

  12. 3-D Clockwise Rotation cos(β)∙cos(γ) cos(β)∙sin(γ) sin(β) -sin(α)∙sin(β)∙cos(γ)-cos(α)∙sin(g) -sin(α)∙sin(β)∙sin(γ)+cos(α)∙cos(γ) sin(α)∙cos(β) -cos(α)∙sin(β)∙cos(γ)+sin(α)∙sin(g) -cos(α)∙sin(β)∙sin(γ)-sin(α)∙cos(γ) cos(α)∙cos(β)

  13. Rotate 3-D function X1=rotate_3da(X,a,b,g) [m,n]=size(X); j=1; if n==3; X=X'; j=2; end Rx = [ 1 0 0 % Roll 0 cos(a) sin(a) 0 -sin(a) cos(a)]; Ry = [ cos(b) 0 sin(b) % Pitch 0 1 0 -sin(b) 0 cos(b)]; Rz = [ cos(g) sin(g) 0 % Yaw -sin(g) cos(g) 0 0 0 1]; R = Rx*Ry*Rz; % R = [ cos(b)*cos(c), cos(b)*sin(c), sin(b) % - cos(a)*sin(c) - cos(c)*sin(a)*sin(b), cos(a)*cos(c) - sin(a)*sin(b)*sin(c), cos(b)*sin(a) % sin(a)*sin(c) - cos(a)*cos(c)*sin(b), - cos(c)*sin(a) - cos(a)*sin(b)*sin(c), cos(a)*cos(b)] X1=R*X; if j==2; X1=X1'; end end

  14. Exercise 1 • Assume we measure the flow from a boat that pitches and rolls because of the wave motion. • The data are measured in a ship coordinate frame (x,y,z) and the flow is ux=10cm, uy=14cm, uz=5cm. • The heading of the boat is 120deg (Magnetic north) and the magnetic declination is 8degs W and the pitch and roll are 10 and 12degs (anticlockwise) respectively. • What is the true east, north and upward components of the flow? • What is the magnitude of the current? • ( Write a MATLAB function that does the rotation of the vector and corrects for pitch and roll) y X

  15. Converting from an arbitrary (non-orthogonal) coordinate system to a Cartesian coordinate system

  16. Doppler Effect is used to measure velocities along the direction of the acoustic wave propagation (1-D) λ2 λ λ1 c=λ·f c=λ·f c-u=λ·f1 c+u=λ·f2 f1 <f2 f1 =f-Δf f2 =f+Δf c-u=λ·f1 c+u=λ·f2

  17. 1-D Doppler current metersPrinciple of operation c : speed of sound in water (depends on T and S) Fo : Frequency of sound transmitted by instrument Df: Doppler shift due to current V V : current speed along the direction of sound propagation Images from: Sontek/YSI

  18. 3-D Doppler current metersPrinciple of operation w v V2 V1 c : speed of sound in water (depends on T and S) Fo : Frequency of sound transmitted by instrument Dfi: Doppler shift due to current Vi along beam direction Vi : current speed along the direction of sound propagation (beam i) V3 u Image from: Sontek/YSI

  19. Acoustic beam current meters

  20. Three Beam to 3-D phi(1) = AOC1 theta (1)= D1OB1 z phi(2) = AOC2 theta (2)= D1OB2 y C2 C1 A B2 B1 x D2 O D1 C3 phi(3) = AOC3 theta (3)= D1OB3 B3

  21. Rotation from arbitrary system to orthogonal coordinate system function T=rotation_matrix(phi,theta) % % phi (in degs) = angle of beam from vertical (z) axis % (phi 1 if the same angle for all beams or % size(phi)=3 if each beam has a different angle % theta (in degs) = angle of beam projection(s) to plane from x, measured counterclockwise % % Vi=T*V and V=inv(T)*Vi % where V=[u,v,w]'; vector of velocities along the x,y,z axis % Vi=[v1,v2,v3]' ; vector of along beam 1, 2 and 3 velocities % % N=length(phi); if N==1; phi=ones(3,1)*phi*pi/180; elseif N==3 phi=phi*pi/180; else error('The Beam angles must be 1 or 3') end phi=phi(:); theta=theta*pi/180; % T(1,:)=[sin(phi(1))*cos(theta(1)) sin(phi(1))*sin(theta(1)) cos(phi(1))]; T(2,:)=[sin(phi(2))*cos(theta(2)+theta(1)) sin(phi(2))*sin(theta(2)+theta(1)) cos(phi(2))]; T(3,:)=[sin(phi(3))*cos(theta(3)+theta(1)) sin(phi(3))*sin(theta(3)+theta(1)) cos(phi(3))];

  22. Two Beam to 3-D phi(1) = AOC1 theta (1)= D1OB1 z phi(2) = 0 theta (2)= 0 y C1 A B1 x O D1 C3 phi(3) = AOC3 theta (3)= D1OB3 B3

  23. Find the mean downstream velocity (Ux) y -10cm/s x 13cm/s 125degs 85degs

More Related