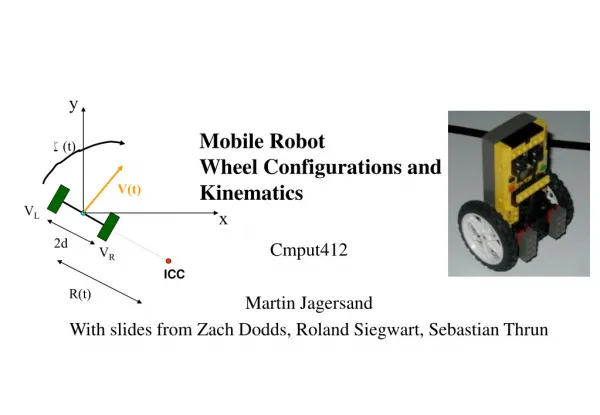
Robot Kinematics II
1.05k likes | 3.06k Vues
Introduction to ROBOTICS. Robot Kinematics II. Dr. Jizhong Xiao Department of Electrical Engineering City College of New York jxiao@ccny.cuny.edu. Kinematics Model. Forward (direct) Kinematics Inverse Kinematics. Forward Kinematics. more generally

Robot Kinematics II
E N D
Presentation Transcript
Introduction to ROBOTICS Robot Kinematics II Dr. Jizhong Xiao Department of Electrical Engineering City College of New York jxiao@ccny.cuny.edu
Kinematics Model • Forward (direct) Kinematics • Inverse Kinematics
Forward Kinematics more generally the forward kinematics problem has been reduced to matrix multiplication
Denavit-Hartenberg Convention • Number the joints from 1 to n starting with the base and ending with the end-effector. • Establish the base coordinate system. Establish a right-handed orthonormal coordinate system at the supporting base with axis lying along the axis of motion of joint 1. • Establish joint axis. Align the Zi with the axis of motion (rotary or sliding) of joint i+1. • Establish the origin of the ith coordinate system. Locate the origin of the ith coordinate at the intersection of the Zi & Zi-1 or at the intersection of common normal between the Zi & Zi-1 axes and the Zi axis. • Establish Xi axis. Establish or along the common normal between the Zi-1 & Zi axes when they are parallel. • Establish Yi axis. Assign to complete the right-handed coordinate system. • Find the link and joint parameters
Z3 Z1 Z0 Joint 3 X3 Y0 Y1 Z2 d2 Joint 1 X0 X1 X2 Joint 2 Y2 a0 a1 Example I • 3 Revolute Joints end-effector frame Link 1 Link 2
Z3 Z1 Z0 Joint 3 X3 Y0 Y1 Z2 d2 Joint 1 X0 X1 X2 Joint 2 Y2 a0 a1 Link Coordinate Frames • Assign Link Coordinate Frames: • To describe the geometry of robot motion, we assign a Cartesian coordinate frame (Oi, Xi,Yi,Zi) to each link, as follows: • establish a right-handed orthonormal coordinate frame O0 at the supporting base with Z0 lying along joint 1 motion axis. • the Ziaxis is directed along the axis of motion of joint (i + 1), that is, link (i + 1) rotates about or translates along Zi; Link 1 Link 2
Z3 Z1 Z0 Joint 3 X3 Y0 Y1 Z2 d2 Joint 1 X0 X1 X2 Joint 2 Y2 a0 a1 Link Coordinate Frames • Locate the origin of the ith coordinate at the intersection of the Zi & Zi-1 or at the intersection of common normal between the Zi & Zi-1 axes and the Zi axis. • the Xiaxis lies along the common normal from the Zi-1 axis to the Ziaxis , (if Zi-1 is parallel to Zi, then Xiis specified arbitrarily, subject only to Xibeing perpendicular to Zi);
Z3 Z1 Z0 Joint 3 X3 Y0 Y1 Z2 d2 Joint 1 X0 X1 X2 Joint 2 Y2 a0 a1 Link Coordinate Frames • Assign to complete the right-handed coordinate system. • The hand coordinate frame is specified by the geometry of the end-effector. Normally, establish Zn along the direction of Zn-1 axis and pointing away from the robot; establish Xn such that it is normal to both Zn-1 and Zn axes. Assign Yn to complete the right-handed coordinate system.
Denavit J and Hartenberg RS, “A kinematic notation for lower-pair mechanisms based on matrices.” Trans ASME J. Appl. Mech, 23:215–221, 1955 • described a convention for standardizing the attachment of frames on links of a serial linkage • common convention for attaching reference frames on links of a serial manipulator and computing the transformations between frames
Denavit-Hartenberg • notice the form of the rotation component • this does not look like it can represent arbitrary rotations • can the DH convention actually describe every physically possible link configuration?
Denavit-Hartenberg • yes, but we must choose the orientation and position of the frames in a certain way • (DH1) • (DH2) • claim: if DH1 and DH2 are true then there exists unique numbers
Denavit-Hartenberg Forward Kinematics • RPP cylindrical manipulator • http://strobotics.com/cylindrical-format-robot.htm
Denavit-Hartenberg Forward Kinematics How do we place the frames?
Step 1: Choose the z-axis for each frame recall the DH transformation matrix
Step 1: Choose the z-axis for each frame link i link i link i+1 link i+1 joint i+1 joint i+1 axis of actuation for joint i+1
Step 1: Choose the z-axis for each frame • Warning: the picture is deceiving. We do not yet know the origin of the frames; all we know at this point is that each zi points along a joint axis
Step 2: Establish frame {0} • place the origin o0 anywhere on z0 • often the choice of location is obvious • choose x0 and y0 so that {0} is right-handed • often the choice of directions is obvious
Step 3: Iteratively construct {1}, {2}, ... {n-1} • using frame {i-1} construct frame {i} • DH1: xi is perpendicular to zi-1 • DH2: xi intersects zi-1 • 4 cases to consider depending on the relationship between zi-1 and zi
Step 3: Iteratively construct {1}, {2}, ... {n-1} (out of page) shortest line between and point of intersection • Case 1 • zi-1 and zi are not coplanar (skew) • ai angle from zi-1 to zi measured about xi
Step 3: Iteratively construct {1}, {2}, ... {n-1} point of intersection • Case 2 • zi-1 and zi are parallel ( ai = 0 ) • notice that this choice results in di = 0
Step 3: Iteratively construct {1}, {2}, ... {n-1} point of intersection (out of page) • Case 3 • zi-1 and zi intersect ( ai = 0 )
Step 3: Iteratively construct {1}, {2}, ... {n-1} (out of page) • Case 4 • xi cannot be perpendicular on zi-1, then xi perpendicular on zi-1 and zi
Step 4: Place the end effector frame “sliding” “normal” “approach”
Step 5: Find the DH parameters • Joint angle : the angle of rotation from the Xi-1 axis to the Xi axis about the Zi-1 axis. It is the joint variable if joint i is rotary. • Joint distance : the distance from the origin of the (i-1) coordinate system to the intersection of the Zi-1 axis and the Xi axis along the Zi-1 axis. It is the joint variable if joint i is prismatic. • Link length : the distance from the intersection of the Zi-1 axis and the Xi axis to the origin of the ith coordinate system along the Xi axis. • Link twist angle : the angle of rotation from the Zi-1 axis to the Zi axis about the Xi axis.
Step 5: Find the DH parameters * joint variable
Step 6: Compute the transformation * joint variable once the DH parameters are known, it is easy to construct the overall transformation
Step 6: Compute the transformation * joint variable
Step 6: Compute the transformation * joint variable
Step 5: DH Parameters * joint variable
Z3 Z1 Z0 Joint 3 X3 Y0 Y1 Z2 d2 Joint 1 X0 X1 X2 Joint 2 Y2 a0 a1 Example I D-H Link Parameter Table : rotation angle from Zi-1 to Zi about Xi : distance from intersection of Zi-1 & Xi to origin of i coordinate along Xi : distance from origin of (i-1) coordinate to intersection of Zi-1 & Xi along Zi-1 : rotation angle from Xi-1to Xi about Zi-1
Example II: PUMA 260 • Number the joints • Establish base frame • Establish joint axis Zi • Locate origin, (intersect. of Zi & Zi-1) OR (intersect of common normal & Zi ) • Establish Xi,Yi t PUMA 260
J 1 -90 0 13 2 0 8 0 3 90 0 -l 4 -90 0 8 5 90 0 0 6 0 0 t Link Parameters : angle from Xi-1to Xi about Zi-1 : angle from Zi-1 to Zi about Xi : distance from intersection of Zi-1 & Xi to Oialong Xi Joint distance : distance from Oi-1 to intersection of Zi-1 & Xi along Zi-1