1 / 75

Algebra 2: Unit 5 Continued

Dive into the fundamentals of factoring quadratic expressions with this comprehensive lesson. Learn what factors are, discover how to find the greatest common factor (GCF), and apply various techniques to factor quadratic expressions effectively. This lesson covers both scenarios where the leading coefficient is 1 and where it isn’t, ensuring thorough understanding. Practice problems are included to solidify your skills, along with strategies for solving quadratic equations through factoring, graphing, and using the quadratic formula.

randall-baxter
Télécharger la présentation

Algebra 2: Unit 5 Continued

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Algebra 2: Unit 5 Continued Factoring Quadratic expression

  2. Factors Factors are numbers or expressions that you multiply to get another number or expression. Ex. 3 and 4 are factors of 12 because 3x4 = 12

  3. Factors What are the following expressions factors of? 1. 4 and 5? 2. 5 and (x + 10) 3. 4 and (2x + 3) 4. (x + 3) and (x - 4) 5. (x + 2) and (x + 4) 6. (x – 4) and (x – 5)

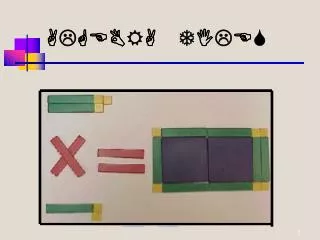
  4. GCF One way to factor an expression is to factor out a GCF or a GREATEST COMMON FACTOR. EX: 4x2+ 20x – 12 EX: 9n2 – 24n

  5. Try Some! Factor: 9x2 +3x – 18 7p2 + 21 4w2 + 2w

  6. Factors of Quadratic Expressions When you multiply 2 binomials: (x + a)(x + b) = x2 + (a +b)x + (ab) This only works when the coefficient for x2 is 1.

  7. Finding Factors of Quadratic Expressions When a = 1: x2+ bx + c Step 1. Determine the signs of the factors Step 2. Find 2 numbers that’s product is c, and who’s sum is b.

  8. Sign table!

  9. Examples Factor: 1. X2 + 5x + 6 2. x2 – 10x + 25 3. x2 – 6x – 16 4. x2 + 4x – 45

  10. Examples Factor: 1. X2 + 6x + 9 2. x2 – 13x + 42 3. x2 – 5x – 66 4. x2 – 16

  11. More Factoring! When a does NOT equal 1. Steps Slide Factor Divide Reduce Slide

  12. Example! Factor: 1. 3x2 – 16x + 5

  13. Example! Factor: 2. 2x2+ 11x + 12

  14. Example! Factor: 3. 2x2+ 7x – 9

  15. Try Some! Factor 1. 5t2 + 28t + 32 2. 2m2 – 11m + 15

  16. March 20th Warm Up Find the Vertex, Axis of Symmetry, X-intercept, and Y-intercept for each: y = x2 + 8x + 9 y= 2(x – 3)2 + 5

  17. Quadratic Equations

  18. Quadratic Equation Standard Form of Quadratic Function: y = ax2 + bx + c Standard Form of Quadratic Equation: 0 = ax2 + bx + c

  19. Solutions A SOLUTION to a quadratic equation is a value for x, that will make 0 = ax2 + bx + c true. A quadratic equation always have 2 solutions.

  20. 5 ways to solve There are 5 ways to solve quadratic equations: Factoring Finding the Square Root Graphing Completing the Square Quadratic Formula

  21. SOLVING BY FACTORING

  22. Factoring Solve by factoring; 2x2 – 11x = -15

  23. Factoring Solve by factoring; x2 + 7x = 18

  24. Factoring Solve by factoring; 1. 2x2 + 4x = 6 2. 16x2 – 8x = 0 3. x2 – 9x + 18 = 0

  25. Solving by Finding Square Roots For any real number x; X2 = n x = Example: x2 = 25

  26. Solve Solve by finding the square root; 5x2 – 180 = 0

  27. Solve Solve by finding the square root; 4x2 – 25 = 0

  28. Try Some! Solve by finding the Square Root: 1. x2 – 25 = 0 2. x2 – 15 = 34 3. x2 – 14 = -10 4. (x – 4)2 = 25

  29. Quadratic Equations Solving by Graphing

  30. Warm Up March 21st A model for a company’s revenue is R = -15p2 + 300p + 12,000 where p is the price in dollars of the company’s product. What PRICE will maximize the Revenue? What is the maximum revenue? Convert to vertex form: y = 2x2 + 6x - 8

  31. 5 ways to solve There are 5 ways to solve quadratic equations: Factoring Finding the Square Root Graphing Completing the Square Quadratic Formula

  32. Solving by Graphing For a quadratic function, y = ax2 +bx + c, a zero of the function, or where a function crosses the x-axis, is a solution of the equations ax2 + bx + c = 0

  33. Examples Solve x2 – 5x + 2 = 0

  34. Examples Solve x2 + 6x + 4 = 0

  35. Examples Solve 3x2 + 5x – 12 = 8

  36. Examples Solve x2 = -2x + 7

  37. Complex Numbers

  38. Quick Review Simplifying Radicals If the number has a perfect square factor, you can bring out the perfect square. EX:

  39. Try Some

  40. Try this: Solve the following quadratic equations by finding the square root: 4x2 + 100 = 0 What happens?

  41. Complex Numbers

  42. Imaginary Number:i The Imaginary number This can be used to find the root of any negative number. EX

  43. Properties of i This pattern repeats!!

  44. Graphing Complex Number

  45. Absolute Values

  46. Operations with Complex Numbers The Imaginary unit, i, can be treated as a variable Adding Complex Number EX: (8 + 3i) + ( -6 + 2i)

  47. Try Some! 7 – (3 + 2i) (4 – 6i) + 3i

  48. Operations with Complex Numbers Multiplying Complex Numbers:Example: (5i)(-4i) Example: (2 + 3i)(-3 + 5i)

  49. Try Some! (6 – 5i)(4 – 3i) (4 – 9i)(4 + 3i)

  50. Now we can SOLVE THIS! Solve 4x2 + 100 = 0

More Related