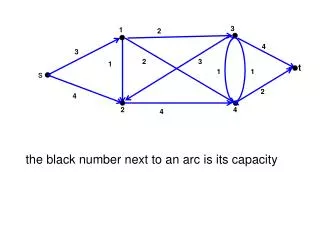
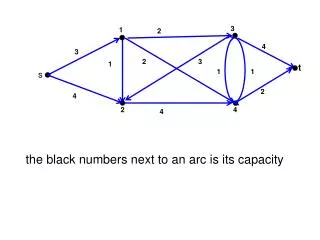
Augmenting path - PowerPoint PPT Presentation
View Augmenting path PowerPoint (PPT) presentations online in SlideServe. SlideServe has a very huge collection of Augmenting path PowerPoint presentations. You can view or download Augmenting path presentations for your school assignment or business presentation. Browse for the presentations on every topic that you want.