1 / 41

Maximum Flow

Maximum Flow. 26.1 流量網路與流量. Flow network( 流量網路 ) G=(V,E) 是一個有向圖，每一邊 (u,v) ∈ E 均有 Capacity( 容量 ) c(u,v)>0 。如 c(u,v)=0 即代表 (u,v) ∉ E 。. c(s,t)=0 ，因 (s,t) ∉ E. v 1. v 3. s. t. v 2. v 4. 流量網路與流量. 令 s 為 Source vertex ， t 為 Sink vertex 。一個 Flow( 流量 ) 係一函數 f ： V×V R ，對任兩點 u,v 而言滿足下列性質：

siran
Télécharger la présentation

Maximum Flow

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

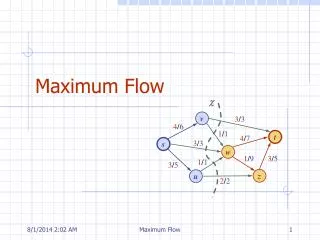
  1. Maximum Flow

  2. 26.1 流量網路與流量 • Flow network(流量網路) G=(V,E)是一個有向圖，每一邊(u,v)∈E均有Capacity(容量) c(u,v)>0。如c(u,v)=0即代表(u,v)∉E 。 c(s,t)=0，因(s,t) ∉ E v1 v3 s t v2 v4

  3. 流量網路與流量 • 令s為Source vertex，t為Sink vertex。一個Flow(流量)係一函數f：V×VR，對任兩點u,v而言滿足下列性質： • Capacity constraint: f(u,v)≤c(u,v) • Skew symmetric: f(u,v)=-f(v,u) • Flow conservation: 若u∈V-{s,t}，則Σw∈Vf(u,w)=0。 • |f|=Σv∈Vf(s,v)稱作流量f的值。

  4. 最大流量問題 • 給一流量網路G，Source s以及Sink t。求出具有最大值的流量f。 12/12 v1 v3 11/16 15/20 f(u,v)/c(u,v) 1/4 s 0/10 t 7/7 4/9 8/13 4/4 v2 v4 11/14

  5. Residue Network與Augmenting Path • 由一Flow network G及一Flow f所導出的Residue network Gf為一個Flow network，其Capacity cf(u,v)=c(u,v)-f(u,v)。 • 一個Flow network G及Flow f所導出的Augmenting path即是Residue network Gf上一個st的路徑p。

  6. Residue Network與Augmenting Path • 如果一Flow network找的到Augmenting path代表可以找到一個Flow f，其值大於0。 • 如一Flow network G及一Flow f所導出的Residue network Gf，以找不到任何Augmenting path，則f是最大流量。

  7. Flow network 12/12 v1 v3 15/20 11/16 f(u,v)/c(u,v) 1/4 t s 0/10 4/9 7/7 v2 v4 3/4 7/13 10/14 12 15 Residue Network v1 v3 5 5 11 4 3 t s 11 7 5 7 1 10 v2 v4 6 3 4 Augmenting Path

  8. 26.2 Ford-Fulkerson演算法 • 主要是利用Residue network的觀點來找出Maxium flow。 • 重複下列動作直到找不到Augmenting path為止。 • 找出Augmenting path p。 • 將Flow f沿著p增加min{cf(u,v):(u,v)在p上}，即residue network Gf中路徑p上最小的Capacity。

  9. Ford-Fulkerson(G,s,t) { for each edge (u,v)∈E[G] do f[u,v]0 f[v,u]0 while∃ path p from s to t on Gf do cf(p)min{cf(u,v):(u,v) is in p} for each (u,v) in p do f[u,v]f[u,v]+cf(p) f[v,u]-f[u,v] return f }

  10. 12 v1 v3 (a) 16 20 s 10 4 t 7 9 13 4 v2 v4 14 4/12 v1 v3 4/16 20 s 10 4 t 7 4/9 13 4/4 v2 v4 4/14

  11. 8 (b) v1 v3 12 4 20 4 4 s 10 t 7 4 5 13 4 10 v2 v4 4 4/12 v1 v3 11/16 7/20 s 4 t 7/10 7/7 4/9 13 4/4 v2 v4 11/14

  12. 8 (c) v1 v3 5 4 13 11 4 7 s 3 t 7 11 5 13 4 3 v2 v4 11 12/12 v1 v3 11/16 15/20 s 10 1/4 t 7/7 4/9 8/13 4/4 v2 v4 11/14

  13. 12 (d) v1 v3 5 5 11 4 15 s 3 t 7 3 5 5 13 4 3 v2 v4 11 12/12 v1 v3 11/16 19/20 s 10 1/4 t 7/7 9 12/13 4/4 v2 v4 11/14

  14. 12 v1 v3 (e) 5 1 11 19 s t 7 11 9 3 1 12 4 3 v2 v4 因無Augmenting path，故Maximum flow如下所示： 12/12 v1 v3 11/16 19/20 s 10 1/4 t 7/7 9 12/13 4/4 v2 v4 11/14

  15. Edmonds-Karp演算法 • 使用Breadth-first search來找Augmenting path。 • 主要能夠避免下面這種情形發生：每次找出的Augmenting path是(s,b,a,t)跟(s,a,b,t)交錯出現，如此要執行2M個Iteration才能做完。 a M M s t 1 M M b

  16. M-1 M a a M M 1 s t s t 1 1 1 M M M b b M-1 M-1 M-1 a a 需要2M次 M M 1 1 s t 1 s t 1 1 1 b M M M-1 M-1 b

  17. Maximum flow and minimum cut • 對一個流量網路G=(V,E)而言，一個Cut (S,T)是將 點集合V分割為S跟T=V-S兩部份且滿足s∈S及t∈T。 • Cut (S,T)的容量(Capacity)，c(S,T)，定義為：所有滿足u∈S及v∈T的邊(u,v)之容量和。

  18. Cut範例 12/12 v1 v3 11/16 15/20 f(u,v)/c(u,v) 1/4 s 0/10 t 7/7 4/9 8/13 4/4 v2 v4 11/14 T S c(S,T)=c(v1,v3)+c(v2,v4) =12+14=26

  19. Lemma 5 Proof:

  20. Corollary 6 Proof:

  21. Maximum flow=minimum cut • 最大流量跟容量最小的Cut是相等的。 • Thm26.6 以下三敘述等價 • (1) f是流量網路G=(V,E)的最大流量 • (2) Residue network Gf找不到Augmenting path • (3) 存在一個Cut (S,T)，|f|=c(S,T)。

  22. Lemma 26.7 Pf: (*)

  23. Thm 26.8 Pf:

  24. There are at most O(E) pairs of vertices that can have an edge • between them in a residual graph, the total number of critical • edges during the entire execution of the Edmonds-Karp • algorithm is O(VE). • Each augmenting path has at least one critical edge, and hence • the theorem follows.

  25. Each iteration of Ford-Fulkerson can be • implemented in O(E) time, when the augmenting • path is found by BFS. • Total running time of the Edmonds-Karp algorithm • is O(VE2). Asymptotically fastest to date for maximum-flow：

  26. Minimum cut的應用 • 可用於決定經營投資策略。如開發產品A1需要先購入工具T1,T2，而產品A2需要先購入工具T2T3，則同時開發僅需要負擔T1,T2,T3的成本。 • 可以將此問題一般化，假定產品Ai需要先購入k個工具Ti1Ti2…Tik。而產品Ai開發完成可獲利Pi，購入工具Tj需要Qj的金錢，則該選擇哪些產品開發？

  27. 利用Minimum cut T1 A1 P1 Q1 T2 A2 Q2 P2 …………. …………. s t Pn-1 Qm-1 Tm-1 An-1 Pn Qm Tm An 如Ai需要Tj，則自T1拉一條容量無限大的邊到Ai。

  28. 流量網路的建構方式 • 將圖如上頁一般的建構出來，有source s, sink t，以及每一個產品與工具。 • 對每個工具Tj自s拉一條容量為Qj的邊。 • 自每一個產品Ai拉一條容量為Pi的邊到t。 • 如Ai需要Tj，則自T1拉一條容量無限大的邊到Ai。

  29. 與最大獲利的對應 • 所有產品的利潤總和扣掉該圖的minimum cut即是最大獲利。 • 觀察：能夠獲利的產品，獲利必然比投入的工具成本高，故將此類的產品與工具劃入T，其他的劃入S。 • 理想的狀態是所有的產品利潤全得，沒有投入的產品部份係扣除產品接到sink的容量，而有投入的產品需扣除投入的工具成本，故扣除source接到工具的容量。所扣除部分即為cut的容量。

  30. 需投入成本 T1 A1 T P1 Q1 T2 A2 Q2 P2 …………. …………. s t Pn-1 Qm-1 Tm-1 An-1 Pn S Qm Tm An 得不到獲利

  31. 26.3 Maximum Bipartite Matching • 一個Bipartite Graph G=(V=L∪R,E)，具有下列性質： • V可以分割成L及R=V-L兩個集合。 • 所有的邊(u,v)的兩個端點u及v不會同在L或同在R之中。

  32. Bipartite Graph範例 L R

  33. Matching • 對一個圖G=(V,E)所謂的配對(Matching)是一個不共用點的邊子集合。即： • 對任意兩邊(u1,v1)，(u2,v2)而言，u1,v1,u2,v2四點均相異。 • 最大配對(Maximum matching)是指具有最多邊的配對。

  34. Matching範例 紅色邊所成的即為一個配對(Matching) L R

  35. Maximum Matching範例 紅色邊所成的即為一個最大配對(Maximum matching) L R

  36. 利用最大流量求最大配對 • 令G’=(V∪{s,t},E∪{(s,u):u∈L}∪{(v,t):v∈R})。即新增source s及sink t進入圖G，並且在s與L的所有點之間拉一條邊，而在R跟t之間拉一條邊。 • 如果所有邊的容量均設定為1，則最大流量等於最大配對。

  37. 流量網路圖 s t L R

  38. 最大流量與最大配對 s t L R

More Related