Time series
230 likes | 617 Vues
Time series. When today has impact on what happens tomorrow. Time series analysis. Statistical time series are data in time, where what happens at one point in time is dependent on what happens at other points in time. T he past and the present give information about the future. Examples:

Time series
E N D
Presentation Transcript
Time series When today has impact on what happens tomorrow
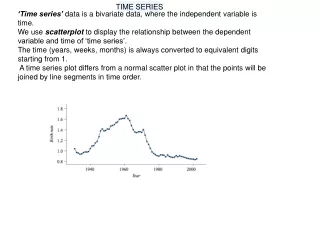
Time series analysis Statistical time series are data in time, where what happens at one point in time is dependent on what happens at other points in time. The past and the present give information about the future. Examples: • population size • the state of the environment, for instance river discharge • the state of a single organism • the number of organisms in a given state • gene frequency • the phenotype (such as bodysize) of a lineage in deep time • the number of species in a clade in deep time etc, etc, etc. discharge time Implicit time dependency: When there is dependency between what happens at one time point and another, even when we check for explicit time. This is what I’m looking at here. Explicit time dependency: When the system is a function of time with only independent noise in addition (typical in physics). Ordinary statistical regression suffices.
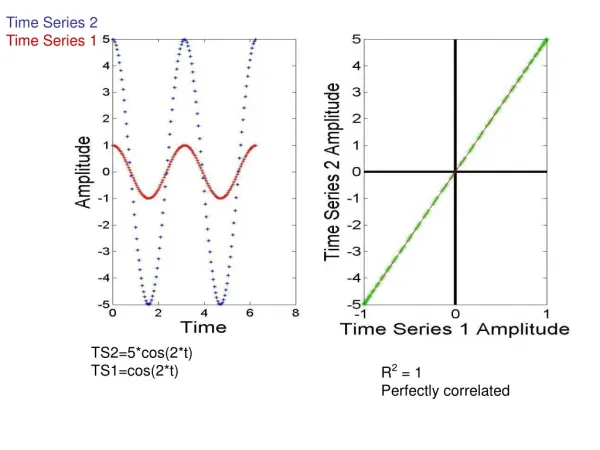
When model clashes with reality – Regression between times series Checking for correlation between two datasets using standard statistical regression analysis can often go wrong, when each dataset is a time series. This is because the model assumptions (independence) are not present. Uncertainties are typically underestimated. A test comparing how many standard errors away from zero the estimate is (score test), can then easily say there’s dependency even if there isn’t. Here are two independently simulated time series. If we plot one against the other, we may easily be led to think there’s dependency between the two series. In this case, a linear regression supports this. But this is only caused by both series being time series! Result from R, summary(lm(x2~x1)): x1 -0.47232 0.04747 -9.95 < 2e-16 ***
When model clashes with reality – independent noise vs time series The “reality”: A simulated “water temperature” with expectation (long term average value) =10. Assume overall variance, =2. Wish to estimate and test whether =10. Model 1, independence: Ti=+i, i~N(0,1) i.i.f. • The graph seems to be telling a different story... • Estimated: • 95% conf. int. for : (11.02,11.80). =10 rejected with 95% confidence! • Model 2, auto-correlated model with expectation , standard devitation and auto-correlation a. • Linear dependency betweentemperature one day and the next. Ti=aTi-1+(1-a)+i, i~N(0,1) i.i.f. • Estimated: • 95% conf. int. for : (9.2,13.6). =10 not rejected.
How to detect time dependency There are several ways to get a glimpse into the nature of a time series (X1,…,Xn): • Auto-correlation. Estimated correlation between Xt and Xt+lag. Simple test: Do the first autocorrelations go beyond +/-1.96/n? • Fourier analysis: Decomposition of a time series into trigonometric contributions with different periodicity. No time dependency => white noise. Periodicity: Some peaks will stand out. Auto correlation: Some kind of pattern. • Statistical model comparison
Strategies for dealing with time dependency • Aggregate the data until you can assume time independence. • Pro: Easy to do • Con: You’ll easily throw the baby out with the bath water. Also, some people may be curious about the nature of the time dependencies. Also, you don’t know in advance how long an aggregation interval you need to assume time independence. • Use standard statistical analysis on models that allows for time dependency and that is reasonable for your data. • Pro: If done properly, nobody can fault you for it. • Con: You’ll need to be able to do statistical analysis and quite possibly also programming. (OpenBUGS/R/Matlab/SAS/C/C++/Fortran). Modeling can be complicated. • Find tools for time series analysis that are suitable (as defined by what kind of time series model you think is reasonable). • Pro: If you know enough to find an analysis tool that supports the kind of modeling that is needed, this is just as good as point 2. If you are good at searching for such tools, this can be time efficient. • Con: You need to be good at searching and possibly you’ll need some pre-knowledge about what words to search for. Also, it may be tempting to pick the first tool that one finds without thinking about whether the model behind accurately represents your data. Also, sometimes the model may not be adequately described by the tool makers. I’m directing this lecture towards strategy 2, but will focus mostly on the modeling, so that it’s also relevant for strategy 3. Note that finding suitable statistical models is a big part of the work.
A simple auto-regressive model, AR(1) Let’s go back to the autoregressive model used in example 2, which was an AR(1) model: Ti=aTi-1+(1-a)+i, i~N(0,1) i.i.f. So Markov chain: The process only depends on the past through the most recent time point, Ti-1. Can find the likelihood (probability density of the dataset). Stationarity: No matter where you start from, TiN(, 2) when i where , 2= 2/(1-a2). The autocorrelation drops exponentially. You can define a characteristic time as the time needed for the auto correlation to drop below a fixed value (typically below ½ or 1/e).
Data (time series) Using the likelihood, L()=f(D| ) Parameter set Classical: • Estimates: Find the that maximizes L(). The maximum likelihood estimator, , has a several nice properties. Optimization tools: “optim” or “nls” in R. • Estimator uncertainty: This can be (asymptotically) derived from Fisher’s information matrix: • A score test can be used for testing whether a parameter has a given value (for instance zero): • Alternatively, the likelihood ratio test can be used: where k is the difference in number of parameters in the zero hypothesis and the alternative. • Information criteria (AIC, BIC) typically minimize -2l()+complexity penalty term, in order to select between models with different complexity. PS: Nonparametric bootstrapping is typically not an option for time series analysis!
Data (time series) Using the likelihood, L()=f(D| ) Parameter set Bayesian: • Bayesian methods also use the likelihood, but together with a prior distribution for the parameters. • Parameter uncertainty comes out as a distribution. • Tools: WinBUGS/OpenBUGS • Often easier to do for complicated models than classical methods. • Model testing a bit more tricky, but favors parsimonious models even without penalty terms.
Variants of time series processes • The way we build the time series dependency can vary: • Markov chain (next slide) • Hidden Markov chains • Models that use Markov chains as building blocks • Some completely other kind of dependency modeling (Martingales?) • The nature of outcomes we can have, must of course affect the model. • Binary outcomes (Bernouilli) • Categorical outcomes of larger size • Count data up a fixed upper ceiling (typically binomial) • Count data with no fixed upper ceiling (Poisson, negative binomial) • Real valued data (often normal) • Strictly positive real valued data (a log transform brings you back) • Multivariate data (often multinormal) • Models can deal with time in different ways: • Discrete (typically used for equidistant data) time • Continuous time (difficult)
General time series theory:Markov chains I think we can agree. The past is over. – G. W. Bush With time dependency, each new measurement depends on the past. f(T1,…,Tn)=f(T1) f(T2 | T1) f(T3 | T2,T1) … f(Tn | Tn-1,…, T2,T1) The likelihood is the product of all one-step-ahead predictions. Unless we do something to restrict the complexity, it will grow exponentially! Markov-chain: Assume that the future depends on the past and present only through the present: f(Ti | Ti-1,…, T2,T1)= f(Ti | Ti-1) With a single model for all the transitions, the model complexity will be greatly reduced. Can deal with the start by having it as a parameter or by assuming stationarity. You can make a graph showing the dependencies: f(T1,…,Tn)=f(T1) f(T2 | T1) f(T3 | T2) … f(Tn | Tn-1) X1 X2 X3 X4
Markov chains – binary outcomes Let’s say we want to model rain at a given site. We make a threshold so that it’s either raining (R) or not (N). Each day, the time series Xt will be in one of these modes. If it’s raining one day, there’s a probability that it will continue the next day pRR=Pr(Xt=R| Xt-1=R) and a probability it will stop, pNR=Pr(Xt=N| Xt-1=R)=1- pRR. Similarly, if it’s not raining one day: pNN=Pr(Xt=N| Xt-1=N) and pRN=Pr(Xt=R| Xt-1=N)=1- pNN. Parameters: pRN and pRR Stationary: pR= pRN/(1+ pRN- pRR) pRR R pNR pRN N pNN X1=Y X1=N X3=N X4=Y X5=Y X6=Y X7=N L=pR (1-pRR) (1-pRN) pRNpRRpRR(1-pRR) Video: Google ”RUU” +”Markov”
Markov chains – life cycles Markov chains when the outcomes belong to larger sets of categories; Life cycles. Example: The xenomorphs in the Alien movie series: youngling (chestbuster) egg queen facehugger adult Transient states Transition probabilities specified by a matrix (rows=old state, columns= new state. Arrow means a positive transition probability. If the life cycles are age categories, then this plus reproduction rates used for calculating populations sizes in different age categories, gives the Leslie matrix approach. Dead Absorbingstate
Markov chains – the Wright-Fisher model (time dependent binomial model) Counting data outcomes: We have an allele, A, which is neutral, (compared to it’s counterpart a), in a population of N diploid organisms. Of interest: The number of A’s at a given time, Xt, which can vary from 0 to 2N. Probability of an A in any given position in the next generation is independent from the other positions in that generation but proportional to the number of A’s in the previous generation. So There are two absorbing states here, namely 0 and 2N. PS: Even if A was not a neutral allele, you could fit a WF process to the data you had. The likelihood would however be low (compared to a model with differential fitness). The likelihood tells you how well the model predicts the time series data rather than how well it fits. R code for this simulation is Given on my web pages.
Markov chains – the Random Walk A random walk (RW) has real valued outcomes. We start from any position (often X1=0) and then add independent random noise each turn so that. If =0, it is an unbiased RW. If not, it will tend to wander in a given direction. Since we’re constantly adding noise, the variance will become larger and larger. Var(Xt)=t2. It is thus not stationary! (AR(1) is) Random walks have been proposed as null hypothesis for large time scale evolution. Random walks can be defined in continuous time as well as for discrete time. Just as the WF model for count data, RWs can be fitted (perfectly) to any data with continuous outcomes. That doesn’t mean it was a random walk that produced it. PS: It’s easy to see “patterns” that aren’t really there.
ARMA models An ARMA model contains two components: an AutoRegressive part (Markov chain) and a Moving Average part. With only the autoregressive part, this would be a Markov chain (conditioned on the state (Xt-1,…,Xt-p). The extra dependency to past noise terms ruins this. But note that these noise terms are themselves the simplest type of Markov chain, namely one with no dependency on the past whatsoever. Thus ARMA models are put together by components that are Markov chains. Pro: Analysis of ARMA models are implemented in many packages. Con: They tend to be “black box” models. They can be fitted to data, but interpreting these models in the context of the field of study can be hard. Connecting to other time series can be done through so-called “transfer terms”.
Hidden Markov chain models A hidden Markov model contains several “layers” of explanation. You have a state that evolves according to a Markov chain. You are however not able to get accurate measurements of it, but you can get noisy measurements of some of it’s components. X1 X2 X3 Xn State: Y1 Y2 Y3 Yn Observations: time For normal linear models, this is what’s known as the Kalman filter. It’s possible to do inference on the state and derive a likelihood analytically in such cases. For discrete states and outcomes, analytical treatment can also be possible (occupancy modeling). For cases where this can’t be done analytically, you can either use MCMC techniques in Bayesian statistics, or so-called particle filters.
Example using the Kalman filter Three water temperature series measured fairly close to each other. Some of the data was removed . State model: Vectorial AR(1) with correlated noise between the three series. Normal observational noise. The plots show how missing data are filled out and shown together with the inference uncertainty. Since the models allow for correlation between the sites, the temperature at one station informs about the temperature at another. Where there is data missing in all stations, the uncertainty will “bubble” out. Could have used a vectorial AR(1) model, but instead I used it’s continuous time parent, the Ornstein-Uhlenbeck process. With a continuous time model, the state between measurements, can also be inferred.
There are known knowns; there are things we know we know.We also know there are known unknowns; that is to say we know there are some things we do not know.But there are also unknown unknowns – the ones we don't know we don't know. - Donald Rumsfeld Hidden components Not all components of a Markov chain need to be directly measured. If some unmeasured components affect the process you are interested in, then the dynamics of the unmeasured components can affect the dynamics of that process. Auto-correlation of phenotype affected by dynamic optimum vs the same of phenotype with optimum assumed constant. Even after taking into account our ”known unknowns” there could be residual dependencies, suggesting the presence of relevant ”unknown unknowns”. The top layer (the phenotype) will not be Markovian by itself , but will be so conditioned on the processes that affects it. The system as a whole is a Markov chain.
Time series resources • Web page: http://folk.uio.no/trondr/timeseries_course • Books: • Box, Jenkins & Reinsel: Time Series Analysis (This is the book that introduced ARMA models) • Shumway & Stoffer: Time Series Analysis and Its Applications (ARMA models and Fourier analysis) • Taylor & Karlin: An Introduction to Stochastic Modeling (Contains much about finite state Markov models, mostly discrete time but a little about continuous time processes also) • West & Harrison: Bayesian Forecasting and Dynamic Models (Built around the Kalman filter. Hidden Markov Models having linear normal updates and with (mostly) known parameters.)
Continuous time processes events time • The Poisson process: • Independent events • Max one event at a given time point. • If you count the number of events in an interval, it will be Poisson distributed. • The time to the next event, from any given starting point, is exponentially distributed. • Birth-death processes: • Count data (population size). • Max one birth or death at a given time point. • Specified with infinitesimal transition probabilities. • Stochastic differential equations: • Real valued outcomes. • Differential equations plus infinitesimal normal contributions. • Examples: continuous time random walk, Ornstein-Uhlenbeck time