1 / 5

Exponential functions

Exponential functions. A function in which x is in the power is called an exponential function. Exponent is another name for power. The general form is: y = b ( a x ) where a and b are constants and a is positive. The graph of an exponential function is called an exponential curve.

ama
Télécharger la présentation

Exponential functions

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

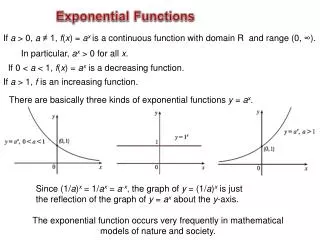
  1. Exponential functions A function in which x is in the power is called an exponential function. Exponent is another name for power. The general form is: y = b(ax) where a and b are constants and a is positive. The graph of an exponential function is called an exponential curve. An asymptote is a line that a curve approaches, but never touches.

  2. y = 10x y = 3x y = 2x All curves of the form ax pass through the point (0,1) Example 1 Sketch the following curves y = 2x 1/8 ¼ ½ 1 2 4 8 y = 3x 1 3 9 27 0·11 0·33 0·037 • Also sketched is 10x and 1·4x. • As the value of a gets bigger the curve gets: • steeper to the right of the y-axis and • closer to x-axis to the left of the y-axis. • The x-axis is an asymptote. y = 1·4x

  3. y = 3(2x) Example 2 y = 2x Sketch the following curves y = 0·3(2x) 0·3 0·6 1·2 2·4 0·04 0·08 0·15 y = 3(2x) 3/8 ¾ 1½ 3 6 12 24 • Also sketched is 2x. • As the value of b gets bigger in y = b(ax): • the curve gets steeper • The curve cuts the y-axis at b instead of 1. y = 0·3(2x)

  4. Example 3 Today’s work y =1·2(2x) -0·3 -0·6 -1·2 -2·4 -4·8 As b is negative the curve is upside down As b is 1·2 the curve cuts the y-axis at 1·2 -9·6 -0·15 Exercise 12 D page 371 #6, 9, 10, 11

More Related