1 / 14

Discrete Cosine Transform.

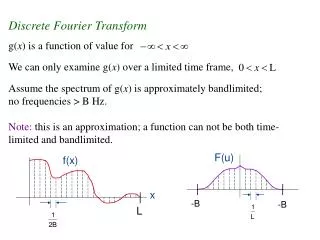
Discrete Cosine Transform. Take our sampled signal and transform it. How? Why?. Basis functions. Like an identi-kit. A series of shapes to create the original waveform. Express the waveform as an amount of the given shapes. The amount of the given shapes is called the co-efficient.

diane
Télécharger la présentation

Discrete Cosine Transform.

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Discrete Cosine Transform. • Take our sampled signal and transform it. • How? • Why?

  2. Basis functions. • Like an identi-kit. • A series of shapes to create the original waveform. • Express the waveform as an amount of the given shapes. • The amount of the given shapes is called the co-efficient.

  3. The DCT formula. • Scary looking formulae: • The equation compares the shape of our sequence xn with a series of cosine shapes. The closer our sequence is to the cosine shape, then the higher X(k) will be.

  4. The cosine shapes for a 4 sample block. • There are as many cosine patterns as there are samples in the sample block. • If we have a four sample block. • Then when: • K=0 • x=1:4;bar(x,cos(0*pi*(2*(x-1)+1)/8)) • K=1 • x=1:4;bar(x,cos(1*pi*(2*(x-1)+1)/8))

  5. The cosine shapes for a 4 sample block. • K=2 • x=1:4;bar(x,cos(2*pi*(2*(x-1)+1)/8)) • K=3 • x=1:4;bar(x,cos(3*pi*(2*(x-1)+1)/8))

  6. Making any sequence from the cosine shapes • Make an arbitrary sequence • Say A=[5 4 –7 2] • Plot a bar graph of it. • We can match this sequence by choosing a certain mixture of our cosine shapes. • We can then completely describe our sequence by the amounts of the cosine shapes alone.

  7. How does it work? • Imagine two shapes defined by a sequence of numbers, such that the numbers defining the shapes each average to zero. • If we multiply the values of a selection of points from any two shapes (defined by a sequence of numbers) together and add up all of the results, then the sum will be zero if the shapes do not correspond to each other, but some non-zero value if there is some correspondence.

  8. Try it • Create two random number sequences in Matlab which average to zero: • a=rand(1,10) - 0.5 • b=rand(1,10) - 0.5 • Plot them on the same graph • plot(a) • hold on • plot(b)

  9. Try it • Multiply each element of a by the corresponding element of b. • c=a.*b (don’t forget the dot) • Sum the result • sum(c) • Now repeat with similar shapes, (make a copy of “a” possibly modify it and plot the new (similar) shape ) multiply “a” by its copy and sum the result. • The more similar the shapes are, the higher the result.

  10. Making any sequence from the cosine shapes • We can therefore calculate the amount of each cosine shape in our sequence by multiplying each value in our sequence by the corresponding value in each of the cosine sequences and summing the result. • X0=cos(0*pi*(2*(x-1)+1)/8) • X1=cos(1*pi*(2*(x-1)+1)/8) • X2=cos(2*pi*(2*(x-1)+1)/8) • X3=cos(3*pi*(2*(x-1)+1)/8) • K0=sum(X0.*A) • K1=sum(X1.*A) • K2=sum(X2.*A) • K3=sum(X3.*A)

  11. Making any sequence from the cosine shapes • Matlab function dct does a discrete cosine transform, that is, it calculates the amount of the cosine shapes that we need to make our sequence. The only difference to our calculation is that the first amount (k=0) is multiplied by the square root of 1/N and the other amounts are multiplied by the square root of 2/N. • Try • dctA= dct(A) • dctA= 2.0 4.9364 5.0 -6.3743

  12. Getting our original shape back (the inverse DCT) • Since we claim that our DCT represents the amount of each cosine shape in our original sequence, then we must be able to reconstruct our original shape by adding the proportions of these shapes together. • Let’s do that. Again we have to use the square root of 1/N and 2/N. • testA1= 2*X0(1)*1/2 + 4.9364*X1(1)*1/2^0.5+ 5.000*X2(1)*1/2^0.5 - 6.3742 * X3(1)*1/2^0.5

  13. Why bother? • We defined our shape with a sequence of numbers originally, why do we want to define it as a new set of numbers representing the amount of similarity to our cosine shapes? • The cosine shapes roughly represent the “frequencies” in the shape (waveform).

  14. Why bother? • Some of these frequencies do not contribute (or occur as frequently) as much as others to the perception of a sound or picture. • If their contribution is low then they can be discarded or coded with fewer bits. (leading to compression). • If some frequencies do not usually take on certain (for example high) values then we can use Huffman coding which leads to compression.

More Related