Download
1 / 12
120 likes | 258 Vues
This guide reviews key concepts of projectile motion, focusing on symmetric and asymmetric scenarios, including football kicks and supply drops from planes. Explore examples that illustrate calculations for maximum height, range, and time of flight using equations of motion. Specifically, analyze a football kicked at an angle, the trajectory of a projectile from a cliff, and how to determine if the ball clears the goalposts. Practice problems from classics like Romeo and Juliet to real-life applications will enhance understanding of physics in motion.
E N D
2-D Examples • Questions on Homework • Review – Football kick (symmetric/asymmetric) • Review – Football field goal (asymmetric) • Review – Range equation (symmetric) • Problem 26 – Plane dropping supplies • Problem 20 – Romeo and Juliet • Problem 31 – Projectile from cliff • Example – High fly ball (simultaneous equations).
Example 4 – Football Kick (symmetric) • Football kicked at 20 m/s and θ = 37 • V0x = 20 cosθ, V0y = 20 sin θ • ax = 0 m/s2, ay = -9.8 m/s2 • Time to maximum height • Maximum height • Velocity at maximum height • Range to maximum height • Time to hit ground • Distance at hit ground • Velocity at hit ground
Example 5 - Football Kick (asymmetric) • Football kicked at 20 m/s @ 37° - 1 m high • Time to hit ground • Distance to hit ground • Eliminate non-physical time
Example 6 – Field Goal (asymmetric) • Will it clear goalposts 3 m high, 30 m from kick? • Strategy • Find time to go 30 m in x direction. • Find how high it is, at that time, in the y direction. • If height greater than 3 m – Field Goal!
Range Equation (symmetric) • X and Y equations • y = ½ gt2 + voyt + yox = voxt + xo • Find time when y = 0 • 0 = ½ gt2 + voyt • t = 0, t = 2voy / g • Then find x • x = voxt = 2voxvoy / g • x = 2vo2sinΘ cosΘ / g • x = vo2sin2Θ / g • Θ = 0 (min), Θ = 90 (min), Θ =45 (max) • Trade-off between x and y motion • Only works for symmetric!!
Problem 27 – Plane dropping supplies • Y equation determines time in air! • Voy = 0 (horizontal flight) • How far will it travel in x given vo. • Must drop that far in advance.
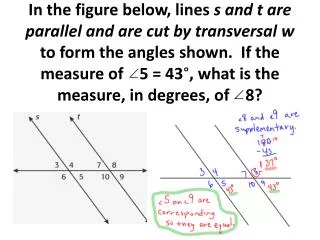
Problem 20 - Romeo and Juliet • What do you know? • vy= 0, y = 4.5 m, a = - 9.8 m/s2 • What tools do you have? • y = ½ at2 + voyt + yo • x = voxt + xo • vy2= voy2 + 2ay • What can you find? • Find voy =9.39 m/s2 • Then find t = 0.958 s (Xwordpuzzle!) • How can you use to find answer? • Given x = 5m, ax = 0 • Know t from above. • vox= vx = x/t = 5.2 m/s.
Example - Simultaneous Equations • Sequential problems • Does the football clear the goal, 3 m high and 30 m from the kick? • Does the high fly clear the fence 10 m high and 95 m from home plate? • Simultaneous problems • When Babe Ruth hit a homer over the 12 m high right-field fence 95 m from home plate, roughly what was the minimum speed of the ball when it left the bat? Assume the ball was hit 1.0 m above the ground and its path initially made a 40° angle with the ground. • 12 m = ½ (-9.8 m/s2) t2 + vo sin(40) t + 1m • 95 m = vocos(40) t • t = 95 m / vocos(40) • t = 3.74 s • vo == 33.16 m/s
Problem 26 – Hunter aims at target • Fired horizontal – How much will miss? • Fired at angle – What angle? • X equation to range • Y equation to zero • Range equation (symmetric)
