Nuclear Magnetic Resonance Spectroscopy

1. Nuclear Magnetic Resonance Spectroscopy An Introduction

2. Over the past fifty years nuclear magnetic resonance spectroscopy, commonly referred to as NMR, has become the preeminent technique for determining the structure of organic compounds. Nuclear magnetic resonance (NMR) spectroscopy: A spectroscopic technique that gives us information about the number and types of nuclei in a molecule. For example, about the number and types of • Hydrogen nuclei using 1H-NMR spectroscopy. • Carbon nuclei using 13C-NMR spectroscopy. • Phosphorus nuclei using 31P-NMR spectroscopy.

3. Nuclear Magnetic Resonance spectroscopy involves the transition of a nucleus from one spin state to another with the resultant absorption of electromagnetic radiation by spin active nuclei when they are placed in a magnetic field. The following features lead to the NMR phenomenon: 1. A spinning charge generates a magnetic field, as shown by the animation on the right. The resulting spin-magnet has a magnetic moment (μ) proportional to the spin.

4. The nuclei of many elemental isotopes have a characteristic spin (I). Some nuclei have integral spins (e.g. I = 1, 2, 3 ....), some have fractional spins (e.g. I = 1/2, 3/2, 5/2 ....), and a few have no spin, I = 0 (e.g. 12C, 16O, 32S, ....). Isotopes of particular interest and use to organic chemists are 1H, 13C, 19F and 31P, all of which have I = 1/2. Since the analysis of this spin state is fairly straightforward, our discussion of NMR will be limited to these and other I = 1/2 nuclei.

6. NUCLEAR SPIN STATES - HYDROGEN NUCLEUS The spin of the positively charged nucleus generates a magnetic moment vector, m. m + + The two states are equivalent in energy in the absence of a magnetic or an electric field. m + 1/2 - 1/2 TWO SPIN STATES

7. In the presence of an external magnetic field (B0), two spin states exist, +1/2 and -1/2. The magnetic moment of the lower energy +1/2 state is alligned with the external field, but that of the higher energy -1/2 spin state is opposed to the external field. Note that the arrow representing the external field points North.

8. Nuclear Spins in Strong External Magnetic Fields N -1/2 In a strong magnetic field (Bo) the two spin states differ in energy. +1/2 Bo S

10. THE ENERGY SEPARATION DEPENDS ON Bo - 1/2 = kBo = hn DE degenerate at Bo = 0 + 1/2 Bo increasing magnetic field strength

11. The Larmor Equation!!! DE = kBo = hncan be transformed into gyromagnetic ratio g g n = 2p frequency of the incoming radiation that will cause a transition Bo strength of the magnetic field g is a constant which is different for each atomic nucleus (H, C, N, etc)

12. More nucleons will be in the lower energy state aligned with the magnetic field. • A nucleon can absorb a quantum of energy in the radio frequency range and align against the magnetic field. • It emits a radio frequency when it drops back to its original position.

13. Absorption of Energy quantized Opposed -1/2 -1/2 DE DE = hn Radiofrequency +1/2 +1/2 Applied Field Bo Aligned

14. A SECOND EFFECT OF A STRONG MAGNETIC FIELD WHEN A SPIN-ACTIVE HYDROGEN ATOM IS PLACED IN A STRONG MAGNETIC FIELD ….. IT BEGINS TO PRECESS OPERATION OF AN NMR SPECTROMETER DEPENDS ON THIS RESULT

16. If rf energy having a frequency matching the Larmor frequency is introduced at a right angle to the external field (e.g. along the x-axis), the precessing nucleus will absorb energy and the magnetic moment will flip to its I = -1/2 state. This excitation is shown in the following diagram.

17. Nuclear Magnetic Resonance • Resonance: In NMR spectroscopy, resonance is due to the absorption of energy by a precessing nucleus and the results in “flip” of its nuclear spin from a lower energy state to a higher energy state. • The precessing spins induce an oscillating magnetic field that is recorded as a signal by the instrument. • Signal: A recording in an NMR spectrum of a nuclear magnetic resonance.

18. Strong magnetic fields are necessary for NMR spectroscopy. The earth's magnetic field is not constant, but is approximately 10-4 T at ground level. Modern NMR spectrometers use powerful magnets having fields of 1 to 20 T. Even with these high fields, the energy difference between the two spin states is less than 0.1 cal/mole.

19. Resonance Frequencies of Selected Nuclei Isotope Abundance Bo (Tesla) Frequency(MHz) g(radians/Tesla) 1H 99.98% 1.00 42.6 267.53 1.41 60.0 2.35 100.0 7.05 300.0 2H 0.0156% 1.00 6.5 41.1 7.05 45.8 13C 1.108% 1.00 10.7 67.28 2.35 25.0 7.05 75.0 19F 100.0% 1.00 40.0 251.7 4:1

20. For NMR purposes, this small energy difference (ΔE) is usually given as a frequency in units of MHz (106 Hz), ranging from 20 to 900 Mz, depending on the magnetic field strength and the specific nucleus being studied. Irradiation of a sample with radio frequency (rf) energy corresponding exactly to the spin state separation of a specific set of nuclei will cause excitation of those nuclei in the +1/2 state to the higher -1/2 spin state. The nucleus of a hydrogen atom (the proton) has a magnetic moment μ = 2.7927, and has been studied more than any other nucleus

21. NMR SPECTROMETER - INSTRUMENTATION

22. DIAMAGNETIC ANISOTROPY SHIELDING BY VALENCE ELECTRONS

23. Bo applied Anisotropy The applied field induces circulation of the valence electrons - this generates a magnetic field that opposes the applied field. valence electrons shield the nucleus from the full effect of the applied field magnetic field lines B induced (opposes Bo) fields subtract at nucleus

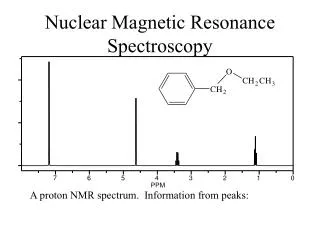
24. SPECTRUM DOWNFIELD UPFIELD Less shielded protons appear here. Highly shielded protons appear here. It takes a higher field to cause resonance. PROTONS DIFFER IN THEIR SHIELDING All different types of protons in a molecule have a different amounts of shielding. They all respond differently to the applied magnetic field and appear at different places in the spectrum. This is why an NMR spectrum contains useful information (different types of protons appear in predictable places).

25. CHEMICAL SHIFT

26. To standardise measurements on different NMR instruments, a standard reference sample is used in each experiment. This is tetramethylsilane (TMS). This is a symmetrical and inert molecule. All H atoms have the same chemical environment and a single peak is produced from this molecule.

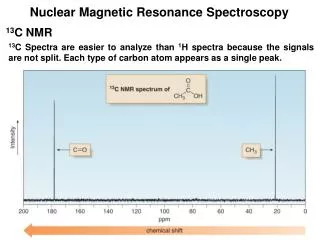
27. The difference in energy needed to change the spin state in the sample is compared to TMS and is called the CHEMICAL SHIFT. • The chemical shift of TMS is defined as zero • The symbol drepresents chemical shift and is measured in ppm. The chemical shift scale is measured from right to left on the spectrum. parts per million shift in Hz chemical shift = d = = ppm spectrometer frequency in MHz This division gives a number independent of the instrument used. A particular proton in a given molecule will always come at the same chemical shift (constant value).

28. NMR Correlation Chart -OH -NH DOWNFIELD UPFIELD DESHIELDED SHIELDED CHCl3 , TMS d (ppm) 12 11 10 9 8 7 6 5 4 3 2 1 0 H CH2Ar CH2NR2 CH2S C C-H C=C-CH2 CH2-C- CH2F CH2Cl CH2Br CH2I CH2O CH2NO2 C-CH-C RCOOH RCHO C=C C C-CH2-C C-CH3 O Ranges can be defined for different general types of protons.

29. IT IS USUALLY SUFFICIENT TO KNOW WHAT TYPES OF HYDROGENS COME IN SELECTED AREAS OF THE NMR CHART C-H where C is attached to an electronegative atom CH on C next to pi bonds aldehyde CHO acid COOH benzene CH alkene =C-H aliphatic C-H 9 12 10 7 6 3 2 0 4 X-C-H X=C-C-H MOST SPECTRA CAN BE INTERPRETED WITH A KNOWLEDGE OF WHAT IS SHOWN HERE

30. Factors influencing the Chemical Shift • Inductive effect by Electronegative groups • Magnetic Anisotropy • Hydrogen Bonding

31. DESHIELDING BY AN ELECTRONEGATIVE ELEMENT d- d+ Chlorine “deshields” the proton, that is, it takes valence electron density away from carbon, which in turn takes more density from hydrogen deshielding the proton. Cl C H d- d+ electronegative element NMR CHART “deshielded“ protons appear at low field highly shielded protons appear at high field deshielding moves proton resonance to lower field

32. Electronegativity Dependence of Chemical Shift Dependence of the Chemical Shift of CH3X on the Element X Compound CH3X CH3F CH3OH CH3Cl CH3Br CH3I CH4 (CH3)4Si Element X F O Cl Br I H Si Electronegativity of X 4.0 3.5 3.1 2.8 2.5 2.1 1.8 Chemical shift d 4.26 3.40 3.05 2.68 2.16 0.23 0 most deshielded TMS deshielding increases with the electronegativity of atom X

33. ANISOTROPIC FIELDS DUE TO THE PRESENCE OF PI BONDS The presence of a nearby pi bond or pi system greatly affects the chemical shift. Benzene rings have the greatest effect.

34. fields add together

35. ANISOTROPIC FIELD IN AN ALKENE protons are deshielded H H Deshielded shifted downfield fields add C=C H H secondary magnetic (anisotropic) field lines Bo

36. ANISOTROPIC FIELD FOR AN ALKYNE H C C H secondary magnetic (anisotropic) field Shielded hydrogens are shielded Bo fields subtract

37. HYDROGEN BONDING DESHIELDS PROTONS The chemical shift depends on how much hydrogen bonding is taking place. Alcohols vary in chemical shift from 0.5 ppm (free OH) to about 5.0 ppm (lots of H bonding). Hydrogen bonding lengthens the O-H bond and reduces the valence electron density around the proton - it is deshielded and shifted downfield in the NMR spectrum.

38. NMR Spectrum of Acetaldehyde offset = 2.0 ppm

39. SPIN-SPIN SPLITTING Often a group of hydrogens will appear as a multiplet rather than as a single peak. Multiplets are named as follows: Singlet Quintet Doublet Septet Triplet Octet Quartet Nonet This happens because of interaction with neighboring hydrogens and is called SPIN-SPIN SPLITTING.

40. 1,1,2-Trichloroethane The two kinds of hydrogens do not appear as single peaks, rather there is a “triplet” and a “doublet”. integral = 2 integral = 1 The subpeaks are due to spin-spin splitting and are predicted by the n+1 rule. triplet doublet

41. this hydrogen’s peak is split by its two neighbors these hydrogens are split by their single neighbor MULTIPLETS singlet doublet triplet quartet quintet sextet septet two neighbors n+1 = 3 triplet one neighbor n+1 = 2 doublet

42. SOME COMMON SPLITTING PATTERNS ( x = y ) ( x = y )

43. INTENSITIES OF MULTIPLET PEAKS PASCAL’S TRIANGLE

44. The interior entries are the sums of the two numbers immediately above. PASCAL’S TRIANGLE Intensities of multiplet peaks 1 singlet 1 1 doublet 1 2 1 triplet 1 3 3 1 quartet 1 4 6 4 1 quintet 1 5 10 10 5 1 sextet 1 6 15 20 15 6 1 septet 1 7 21 35 35 21 7 1 octet

45. THE CHEMICAL SHIFT OF PROTON HA IS AFFECTED BY THE SPIN OF ITS NEIGHBORS aligned with Bo opposed to Bo +1/2 -1/2 50 % of molecules 50 % of molecules H H H H A A C C C C Bo downfield upfield neighbor aligned neighbor opposed At any given time about half of the molecules in solution will have spin +1/2 and the other half will have spin -1/2.

46. SPIN ARRANGEMENTS one neighbor n+1 = 2 doublet one neighbor n+1 = 2 doublet H H H H C C C C yellow spins blue spins The resonance positions (splitting) of a given hydrogen is affected by the possible spins of its neighbor.

47. SPIN ARRANGEMENTS two neighbors n+1 = 3 triplet one neighbor n+1 = 2 doublet methine spins methylene spins

48. H H H H H H C C C C H H H H SPIN ARRANGEMENTS three neighbors n+1 = 4 quartet two neighbors n+1 = 3 triplet methylene spins methyl spins

49. THE COUPLING CONSTANT J J J J J J The coupling constant is the distance J (measured in Hz) between the peaks in a multiplet. J is a measure of the amount of interaction between the two sets of hydrogens creating the multiplet.

50. APPLICATIONS • GEOPHYSICAL: Used to determine the water content in the geophysical samples. • Engineering Applications: It is used to study the Process engineering aspects like the kinetic and equilibrium studies of Formaldehyde – water – methanol systems. • Non- destructive testing of DNA, proteins etc. • This is very much useful in Data acquisition in Petroleum Industry. Here NMR probes are developed and Used.