1 / 30

Reachability Analysis of Sequential Circuit

This study presents a novel approach to reachability analysis in sequential circuits using product finite state machines (FSMs). We propose a method that creates a product FSM from two given FSMs, M1 and M2, to traverse all possible states and check outputs during transitions. The analysis reveals if all outputs are equivalent, indicating equivalence between M1 and M2. Our research underscores the importance of sequential depth in determining the fixed point of FSMs, ensuring all possible states are explored for accurate circuit validation.

hiram-case
Télécharger la présentation

Reachability Analysis of Sequential Circuit

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Reachability Analysis of Sequential Circuit Speaker: Jung-Tai Tsai Advisor: Chun-Yao Wang 2007.5.22 Department of Computer Science National Tsing Hua University, Taiwan 1

  2. Outline • Introduction • Previous Work • Our Approach • Experimental Results • Conclusions and Future Work 2

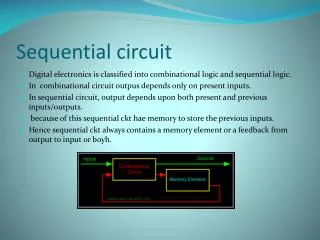
  3. Product Machine • Given two FSMs M1, M2 • Create a product FSM：M= M1 x M2 • Traverse the states of M and check its output for each transition • The output O(M)=1, if output O1 = O2 • If all outputs of M are 1, then M1 ≡ M2 • Otherwise, an error state is reached 3

  4. Why Reachability Analysis • Need to traverse all possible states of product machine and check its output for each transition • If all states have been traversed ,say it reaches the fixed point 4

  5. Sequential Depth • The sequential depth of an FSM is given by the longest path among all shortest paths from the initialstate to all nodes in the STG of FSM • The sequential depth is equal to the number of iterations need to reach the fixed point 5

  6. Problem Formulation • Given: • One sequential netlist • One initial state • Netlists consist of AND2/OR2/NOT/flip-flop • Objective: • Determine the fixed point to guarantee all possible states are traversed 6

  7. Outline • Introduction • Previous Work • Our Approach • Experimental Results • Conclusions and Future Work 7

  8. Previous Work Symbolic: fixed-point Initial state R0 reachable state R1 R2 RK Rk+1 • In conventional terminology, the reachable state set at a time t • refer to the set of all states that are reachable at any time • between 0 and t • The sets of the reachable states in two consecutive iterations are • identical, it reaches a fixed point 8

  9. Outline • Introduction • Previous Work • Our Approach • Experimental Results • Conclusions and Future Work 9

  10. 01001101 01001101 01001101 01001101 01001101 01001101 01001101 01001101 01001101 10000010 10000010 10000010 10000010 10000010 10000010 10000010 10000010 10000010 G0 ˙ G5_in (S0) 01001111 [11] G5 00000000 ˙ ˙ [12] G6_in (S1) o [14] G17 00000000 G6 [17] 00111101 G1 [13] 00000000 G7 00110100 00110100 00110100 00110100 00110100 00110100 00110100 00110100 00110100 G3 10011010 G2 00001001 G7_in (S2) Parallel Random Vector Simulation 0 0 S0 0 0 1 1 0 S1 S1 0 0 1 0 1 1 0 S2 S2 S2 S2 0 0 0 0 1 1 1 0 0 1 1 1 : reached state 1 0 1 1 0 1 0 0 1 : undecided or conflict state 0 10

  11. G0 ˙ G5_in (S0) [11] G5 ˙ ˙ [12] G6_in (S1) o [14] G17 G6 [17] G1 [13] G7 G3 G2 G7_in (S2) Forward Simulation 0 0 0 0 11

  12. G0 ˙ G5_in (S0) [11] G5 ˙ ˙ [12] G6_in (S1) o [14] G17 G6 [17] G1 [13] G7 G3 G2 G7_in (S2) Backward Justification 0 0 0 0 0 S0 0 0 1 0 S1 S1 0 0 1 0 1 S2 S2 S2 S2 0 0 0 0 1 1 0 0 1 1 0 1 1 0 1 0 0 1 12

  13. 01001101 01001101 01001101 01001101 01001101 01001101 01001101 01001101 01001101 10000010 10000010 10000010 10000010 10000010 10000010 10000010 10000010 10000010 G0 ˙ G5_in (S0) 01001111 [11] G5 00000000 ˙ ˙ [12] G6_in (S1) o [14] G17 00000000 G6 [17] 00111101 G1 [13] 00000000 G7 00110100 00110100 00110100 00110100 00110100 00110100 00110100 00110100 00110100 G3 10011010 G2 00001001 G7_in (S2) Controllability Calculation C0= 3/8 C1= 5/8 C0= 8/8 C1= 0/8 C0= 5/8 C1= 3/8 13

  14. conflict conflict Justification Order S0S2S1 S0S1S2 S0 S0 S1 S1 S2 S2 • Choose the harder one to be the first • Lower probability of being the value that stuck in FFs • Conflict may occur early 14

  15. Controllability As Guidance ofBacktrace • Objective (G7_in, 0) • Two possible solutions: G2=1 or [17]=1 • Choose the easier one: [17]=1 (higher probability of being 1) C0= 6/8 C1= 2/8 G2 0 G7_in (S2) [17] C0= 5/8 C1= 3/8 Choose path G7_in → [17]for backtracing 15

  16. G0 ˙ G5_in (S0) [11] G5 ˙ ˙ [12] G6_in (S1) o [14] G17 G6 [17] G1 [13] G7 G3 G2 G7_in (S2) Backward Justification 0 C0= 4/8 0 C1= 4/8 0 C0= 6/8 0 0 1 1 C1= 2/8 0 1 C0= 5/8 S0S2S1 C1= 3/8 1 S0 0 0 0 1 0 S1 S1 0 1 0 1 0 S2 S2 S2 S2 0 C0= 6/8 0 0 1 1 0 0 1 1 C1= 2/8 C0= 5/8 1 0 1 1 0 1 0 0 1 C1= 3/8 16

  17. G0 ˙ G5_in (S0) [11] G5 ˙ ˙ [12] G6_in (S1) o [14] G17 G6 [17] G1 [13] G7 G3 G2 G7_in (S2) conflict Backward Justification C0= 4/8 0 C1= 4/8 0 C0= 6/8 1 0 1 0 C1= 2/8 2/8< 3/8 < 4/8 0 0 S1S2S0 S0 1 0 0 1 0 S1 S1 1 0 1 0 1 S2 S2 S2 S2 1 0 0 0 1 1 1 0 0 1 1 C0= 5/8 1 1 1 0 1 0 0 1 C1= 3/8 17

  18. G0 ˙ G5_in (S0) [11] G5 ˙ conflict ˙ [12] G6_in (S1) o [14] G17 G6 [17] G1 [13] G7 G3 G2 G7_in (S2) Backward Justification C0= 4/8 1 C1= 4/8 0 0 C0= 6/8 1 0 C1= 2/8 2/8< 4/8 0 0 S1S0S2 S0 0 1 1 0 S1 S1 1 0 1 0 1 S2 S2 S2 S2 X 0 0 1 1 1 0 0 1 1 0 1 1 1 0 1 0 0 1 18

  19. initial state=(000) S0 S1 0 S2 S0 S0 0 0 0 1 1 S1 S1 S1 S1 0 0 0 1 1 0 0 1 1 S2 S2 S2 S2 S2 S2 S2 S2 0 0 1 1 1 1 0 0 1 1 1 1 0 0 0 0 Determine Fixed Point t = 0 GlobalBDD 0 0 0 0 0 1 0 0 0 Local BDD Is this disjoint cube subset of global bdd? 1 1 0 0 0 1 1 1 19

  20. 0 0 1 S0 S0 S0 S1 S1 S1 1 0 0 S2 S2 S2 0 X X S0 S0 S0 S0 0 0 0 0 1 1 1 1 S1 S1 S1 S1 S1 S1 S1 S1 0 0 0 0 1 1 1 1 0 0 0 0 1 1 1 1 Local BDD S2 S2 S2 S2 S2 S2 S2 S2 S2 S2 S2 S2 S2 S2 S2 S2 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 1 1 1 1 1 1 1 1 0 0 0 0 0 0 0 0 1 1 1 0 0 1 1 1 Timeframe = 1 t = 1 Local BDD GlobalBDD 0 1 1 0 1 0 0 1 0 0 0 0 1 Local BDD S S S J J 1 1 0 0 0 1 1 1 1 S 1 0 1 0 1 0 0 1 0 0 0 1 20

  21. 1 0 S0 S0 S1 S1 X 0 S2 S2 X X S0 S0 0 0 1 1 S1 S1 S1 S1 0 0 1 1 0 0 1 1 S2 S2 S2 S2 S2 S2 S2 S2 0 0 1 1 1 1 0 0 1 1 1 1 0 0 0 0 Timeframe = 2 t = 2 Local BDD GlobalBDD 0 0 0 1 0 0 1 0 1 0 1 1 0 1 S S S S J J 1 1 0 0 0 1 1 1 1 21

  22. 0 1 S0 S0 S1 S1 X 0 S2 S2 X X S0 0 1 S1 S1 0 1 0 1 S2 S2 S2 S2 0 1 1 0 1 1 0 0 Timeframe = 3 t = 3 GlobalBDD The size of BDD is intact in two consecutive timeframe  reach fixed point 1 1 1 0 0 1 1 1 22

  23. Outline • Introduction • Previous Work • Our Approach • Experimental Results • Conclusions and Future Work 23

  24. Experimental Results 24

  25. 25

  26. 26

  27. Outline • Introduction • Previous Work • Our Approach • Experimental Results • Conclusions and Future Work 27

  28. Conclusions • We use Parallel Random Vector Simulation as the first stage to traverse partial states efficiently in each timeframe • Implication and circuit structure analysis play the roles of determining undecided states • Use BDD to record all traversed states, it reaches a fixed point when the size of BDD is intact in two consecutive timeframe 28

  29. Cont’d • Some heuristic methods accelerate our approache.g., justification order, decision point selection 29

  30. Future Work Experimental results V.S. Corn 30

More Related