1 / 16

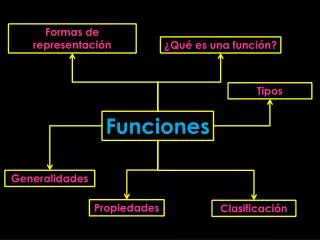
FUNCIONES.

FUNCIONES. UNA FUNCIÓN f, es una correspondencia entre dos conjuntos numéricos A y B, que asocia a cada elemento x de A un solo elemento y de B.

ingrid
Télécharger la présentation

FUNCIONES.

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. FUNCIONES.

  2. UNA FUNCIÓN f, es una correspondencia entre dos conjuntos numéricos A y B, que asocia a cada elemento x de A un solo elemento y de B. Los puntos x e y de una función pueden venir representados por una gráfica sobre los ejes cartesianos, una tabla de valores x e y, o una ecuación de la forma: y = f (x). Donde f(x) es una expresión algebraica que contiene a x como variable. A los elementos x  A, se le denomina VARIABLE INDEPENDIENTE, y a los elementos y  B VARIABLE DEPENDIENTE. FUNCIONES

  3. Ejemplos: La siguiente gráfica corresponde a una función

  4. (0, f(0) ) = ( 0 , 9 ) (-5, f(-5) ) = ( -3 , 0 ) Eje de abcisas Eje de ordenadas (-3, f(-3) ) = ( -3 , 0 ) Ejemplo:

  5. PROPIEDADES GRÁFICAS DE FUNCIONES Una función f(x) es MONÓTONA CRECIENTE en un tramo cuando para cada dos números a, b si a < b, entonces f (a) < f (b). Una función f(x) es MONÓTONA DECRECIENTE en un tramo cuando para cada dos números a, b si a < b, entonces f (a) > f (b). Una función f(x) es MONÓTONA en un tramo cuando es MONÓTONA CRECIENTE ó MONÓTONA DECRECIENTE.

  6. Ejemplo. La siguiente función Es monótona creciente en (0,2) y en (5,8) y monótona decreciente en (2,5).

  7. FUNCIONES DADAS POR TABLAS DE VALORES. Si queremos representar la gráfica de una función aproximadamente a partir de una tabla de valores de las variables independientes x, y de las variables dependientes y. Podemos representar dichos puntos en el plano y unirlos con una línea.

  8. Ejemplo. Conocida la tabla de valores: x y . 0 0 1 1 2 4 3 9 4 16 Podemos representar la siguiente función

  9. Si la pendiente m = b/a Por cada a unidades que avanza x, sube (o baja si es negativo) b unidades b a FUNCIONES DE PROPORCIONALIDAD: y = m x Una función de proporcionalidad es aquella que relaciona dos valores directamente proporcionales. Su ecuación algebraica es de la forma y = m x Se representa por una recta que pasa por el punto (0,0). La constante de proporcionalidad m, puede ser positiva o negativa, y se denomina pendiente o inclinación de la recta.

  10. Ejemplo. Representar y = - 2 x x y . - 1 2 0 0 1 - 2 2 - 4 3 - 6 Y Podemos representar la función

  11. FUNCIONES LINEALES: y = m x + n La ecuación y = m x + n se representa mediante una recta de pendiente m que corta al eje Y en el punto (0,n). n se denomina ordenada en el origen. Dos ecuaciones con las misma pendiente representa rectas paralelas. La función y =m x + n se denomina función lineal. Cuando n = 0 ( y = m x) se trata de una función de proporcionalidad.

  12. Ejemplo. Representar y = - 2 x + 1 x y . - 1 3 0 1 1 - 1 2 - 3 3 - 5 Y Podemos representar la función

  13. FUNCIONES CONSTANTE: y = k La ecuación y = k, en la que y no depende de x. se llama función constante. Se representa por una recta paralela al eje S, a una distancia k de éste. Ejemplo. Representar y = - 2 e y = 1

  14. Mas ayuda del tema de la página Matemática de DESCARTES del Ministerio de Educación y ciencia(http://recursostic.educacion.es/descartes/web/)En la siguiente diapósitiva

More Related