1 / 89

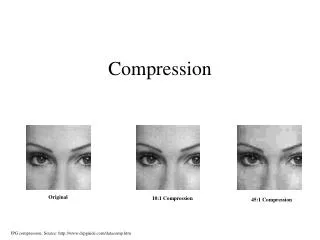
Geometry Compression

Geometry Compression. Michael Deering, Sun Microsystems SIGGRAPH (1995) Presented by: Michael Chung. Geometry Compression What is it?. Lossy technique for reducing the size of geometry representation. Motivation. Save bandwidth and transmission time in graphics accelerators and networks.

jbalderrama
Télécharger la présentation

Geometry Compression

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Geometry Compression Michael Deering, Sun Microsystems SIGGRAPH (1995) Presented by: Michael Chung

  2. Geometry CompressionWhat is it? • Lossy technique for reducing the size of geometry representation.

  3. Motivation • Save bandwidth and transmission time in graphics accelerators and networks. • Save storage space in main memory and on disk.

  4. Proposed Contributions • Technique for lossy compression ratios of between 6 and 10 to 1 • Claims only slight losses in object quality • Depends on original representation format and final quality level desired

  5. Geometry CompressionWhat is it? • Trade-off between quality (subjective) and amount of compression. • Compression steps can be reversed for decompression

  6. Geometry CompressionWhat is it? • Goal: represent geometry with geometry compression instructions

  7. Insights • Reduce size of geometry representation in several ways. • Reuse vertices in triangle strip via reference • Bit shaving • Geometry is local, encode deltas • Normals as indices

  8. Compression Steps • Convert triangle data to generalized triangle mesh • Quantization of positions, colors, normals • Delta encoding of quantized values • Huffman tag-based variable-length encoding of deltas • Output binary output stream with Huffman table initializations and geometry compression instructions

  9. Compression Steps • Convert triangle data to generalized triangle mesh • Quantization of positions, colors, normals • Delta encoding of quantized values • Huffman tag-based variable-length encoding of deltas • Output binary output stream with Huffman table initializations and geometry compression instructions

  10. Step 1: Conversion to Generalized Triangle Mesh generalized triangle strip  generalized triangle mesh • Generalized triangle strip • Specifies vertices with four vertex replacement codes (2 bits): • Replace oldest • Replace middle • Restart clockwise • Restart counterclockwise

  11. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle strip (example)

  12. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle strip (example)

  13. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle strip (example)

  14. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle strip (example)

  15. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle strip (example)

  16. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle strip (example)

  17. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle strip (example)

  18. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle strip (example)

  19. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle strip (example)

  20. Geometry Compression Instruction Set

  21. Geometry Compression Instruction Set

  22. Geometry Compression Instruction Set

  23. Step 1: Conversion to Generalized Triangle Mesh generalized triangle strip  generalized triangle mesh • Generalized triangle mesh • Generalized triangle strip • Mesh buffer • 16 slot queue • 4 bit index • Explicitly push vertices onto mesh buffer for reuse. • We save because only 4 bits are required to reference old vertex.

  24. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle mesh (example)

  25. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle mesh (example)

  26. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle mesh (example)

  27. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle mesh (example)

  28. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle mesh (example)

  29. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle mesh (example)

  30. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle mesh (example)

  31. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle mesh (example)

  32. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle mesh (example)

  33. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle mesh (example)

  34. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle mesh (example)

  35. Step 1: Conversion to Generalized Triangle Mesh • Generalized triangle mesh (example)

  36. Step 1: Conversion to Generalized Triangle Mesh

  37. Step 1: Conversion to Generalized Triangle Mesh

  38. Geometry Compression Instruction Set

  39. Compression Steps • Convert triangle data to generalized triangle mesh • Quantization of positions, colors, normals • Delta encoding of quantized values • Huffman tag-based variable-length encoding of deltas • Output binary output stream with Huffman table initializations and geometry compression instructions

  40. Step 2: Quantization

  41. Step 2: Quantization

  42. Step 2: Quantization • Some parts of the geometry may require more or less precision than others.

  43. Step 2: Quantization • Some parts of the geometry may require more or less precision than others. • So, the amount of quantization we perform per position, normal, and color is variable.

  44. Step 2: Quantization • Position • 32-bit floating-point coordinates are wasteful. • 8-bit exponent allows an unnecessary range of values. • 24-bit fixed-point mantissa offers unnecessary precision.

  45. Step 2: Quantization • Position • Based on empirical visual tests, allow at most 16 bits per component (X, Y, Z)

  46. Step 2: Quantization • Color • Linear reflectivity values R, G, B, (optional) A • Range from 0.0 to 1.0 per component • cap state bit sets alpha ON and OFF • At most 12 unsigned fraction bits per component

  47. Geometry Compression Instruction Set

  48. Step 2: Quantization • Normal • 96 bits can represent up to 296 different normals • We don’t need so many • Angular density of 0.01 radians between normals visually indistinguishable • This is about 100,000 normals distributed over a unit sphere • 48 bits to represent a normal (16 bits per X, Y, Z) • We can do better than 48 bits per normal • Use clever indexing to represent ~100,000 normals with 18 bits…

  49. Step 2: Quantization • Normal • 96 bits can represent up to 296 different normals • We don’t need so many • Angular density of 0.01 radians between normals visually indistinguishable • This is about 100,000 normals distributed over a unit sphere • 48 bits to represent a normal (16 bits per X, Y, Z) • We can do better than 48 bits per normal • Use clever indexing to represent ~100,000 normals with 18 bits…

  50. Step 2: Quantization • Normal • 96 bits can represent up to 296 different normals • We don’t need so many • Angular density of 0.01 radians between normals visually indistinguishable • This is about 100,000 normals distributed over a unit sphere • 48 bits to represent a normal (16 bits per X, Y, Z) • We can do better than 48 bits per normal • Use clever indexing to represent ~100,000 normals with 18 bits…

More Related