Hidden Markov Models
260 likes | 421 Vues
Hidden Markov Models. Eine Einführung. A. T. B. E. C. G. Markov Chains. Markov Chains. We want a model that generates sequences in which the probability of a symbol depends on the previous symbol only. Transition probabilities : Probability of a sequence : Note:. Markov Chains.

Hidden Markov Models
E N D
Presentation Transcript
Hidden Markov Models Eine Einführung
A T B E C G Markov Chains
Markov Chains • We want a model that generates sequences in which the probability of a symbol depends on the previous symbol only. • Transition probabilities: • Probability of a sequence: Note:
Markov Chains • The key property of a Markov Chain is that the probability of each symbol xi depends only on the value of the preceeding symbol • Modelling the beginning and end of sequences
Markov Chains • Markov Chains can be used to discriminate between two options by calculating a likelihood ratio Example: CpG – Islands in human DANN Regions labeled as CpG – islands + model Regions labeled as non-CpG – islands - model Maximum Likelihood estimators for the transition probabilities for each model and analgously for the – model. Cst+ is the number of times letter t followed letter s in the labelled region
Markov Chains • From 48 putative CpG – islands of a human DNA one estimates the following transition probabilities Note that the tables are asymmetric
Markov Chains • To use the model for discrimination one calculates the log-odds ratio
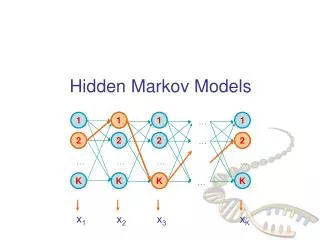
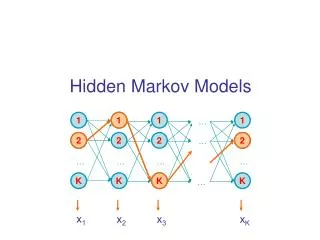
Hidden Markov Models • How can one find CpG – islands in a long chain of nucleotides? • Merge both models into one model with small transition probabilities between the chains. • Within each chain the transition probabilities should remain close to the original ones • Relabeling of the states: The states A+, C+, G+, T+ emit the symbols A, C, G, T • The relabeling is critical as there is no one to one correspondence between the states and the symbols. From looking at C in isolation one cannot tell whether it was emitted from C+ or C-
Hidden Markov Models Formal Definitions • Distinguish the sequence of states from the sequence of symbols • Call the state sequence the path π. It follows a simple Markov model with transition probabilities • As the symbols b are decoupled from the states k new parameters are needed giving the probability that symbol b is seen when in state k These are known as emission probabilities
Hidden Markov Models The Viterbi Algorithm • It is the most common decoding algorithm with HMMs • It is a dynamic programming algorithm • There may be many state sequences which give rise to any particular sequence of symbols • But the corresponding probabilities are very different • CpG – islands: (C+, G+, C+, G+)(C-, G-, C-, G-)(C+, G-, C+, G-) They all generate the symbol sequence CGCG but the first has the highest probability
Hidden Markov Models • Search recursively for the most probable path • Suppose the probability vk(i) of the most probable path ending in state k with observation i is known for all states k • Then this probability can be calculated for state xi+1 by with initial condition
Hidden Markov Models Viterbi Algorithm • Initialisation (i=0): • Rekursion (i=1..L): • Termination: • Traceback (i=1….L):
Hidden Markov Models CpG Islands and CGCG sequence
Hidden Markov Models The Forward Algorithm • As many different paths π can give rise to the same sequence, the probability of a sequencey P(x) is • Brute force enumeration is not practical as the number of paths rises exponentially with the length of the sequence • A simple solution is to evaluate at the most probable path only.
Hidden Markov Models • The full probability P(x) can be calculated in a recursive way with dynamic programming.This is called the forward algorithm. • Calculate the probability fk(i) of the observed sequence up to and including xi under the constraint that πi = k • The recursion equation is
Hidden Markov Model Forward Algorithm • Initialization (i=0): • Recursion (i=1…..L): • Termination:
Hidden Markov Model The Backward Algorithm • What is the most probable state for an observation xi ? • What is the probability P(πi = k | x) that observation xi came from state k given the observed sequence. This is the posterior probability of state k at time i when the emitted sequence is known. • First calculate the probability of producing the entire observed sequence with the ith symbol being produced by state k:
Hidden Markov Model The Backward Algorithm • Initialisation (i=L): • Recursion (i=L-1,…..,1): • Termination:
Hidden Markov Models Posterior Probabilities • From the backward algorithmposterior probabilities can be obtained where P(x) is the result of the forward algorithm.
Hidden Markov Model Parameter Estimation for HMMs • Two problems remain: 1) how to choose an appropriate model architecture 2) how to assign the transition and emission probabilities • Assumption: Independent training sequences x1 …. xn are given • Consider the log likelihood where θ represents the set of values of all parameters (akl,el)
Hidden Markov Models Estimation with known state sequence • Assume the paths are known for all training sequences • Count the number Akl and Ek(b) of times each particular transition or emission is used in the set of training sequences plus pseudocounts rkl and rk(b), respectively. • The Maximum Likelihood estimators for akl and ek(b) are then given by
Hidden Markov Models Estimation with unknown paths • Iterative procedures must be used to estimate the parameters • All standard algorithms for optimization of continuous functions can be used • One particular iteration method is standardly used: the Baum – Welch algorithmus -- first estimate the Akl and Ek(b) by considering probable paths for the training sequences using the current values of the akl and ek(b) -- second use the maximum likelihood estimators to obtain new transition and emission parameters -- iterate that process until a stopping criterium is met -- many local maxima exist particularly with large HMMs
Hidden Markov Models Baum – Welch Algorithmus • It calculates the Akl and Ek(b) as the expected number of times each transition or emission is used in the training sequence • It uses the values of the forward and backward algorithms • The probability that akl is used at position i in sequence x is
Hidden Markov Models Baum – Welch Algorithm • The expected number of times akl is used can be derived then by summing over all positions and over all training sequences • The expected umber of times that letter b appears in state k is given by
Hidden Markov Models Baum – Welch Algoritmus • Initialisation: Pick arbitrary model parameters • Recurrence: Set all A and E variables to their pseudocount values r or to zero For each sequence j=1……n: -- calculate fk(i) for sequence j using the forward algorithm -- calculate bk(i)for sequence j using the backward algorithm -- add the contribution of sequence j to A and E -- calculate the new model parameters maximum likelihood estimator -- calculate the new log likelihood of the model • Termination: stop if log likelihood change is less than threshold
Hidden Markov Models Baum – Welch Algorithm • The Baum – Welch algorithm is a special case of an Expectation – Maximization Algorithm • As an alternative Viterbi training can be used as well. There the most probable paths are estimated with the Viterbi algorithm. These are used in the iterative re-estimation process. • Convergence is garanteed as the assignment of the paths is a discrete process • Unlike Baum – Welch this procedure does not maximise the true likelihood P(x1…..xn|θ) regarded as a function of the model parameters θ • It finds the value of θ that maximizes the contribution to the likelihood P(x1…..xn|θ,π*(x1),….., π*(xn)) from the most probable paths for all sequences.