Density Curves and Normal Distribution

DensityCurves andNormal Distribution Mr. Markwalter

Notagoras’ Theorem • People who keep organized notebooks are doing the best • People who copy down my examples are doing the best • People who ask questions are doing the best • ∴Take our a notebook. No more loose leaf • I will start putting up models for note-taking

So… • We can make histograms of data. • But sometimes we have a lot of data and: THE OVERALL PATTERN OF A LARGE NUMBER OF OBSERVATIONS IS SO REGULAR WE CAN DESCRIBE IT BY A SMOOT CURVE!

Let’s See What I Mean • 947 students tested • Distribution of scores is below

Let’s See What I Mean • We can look at it in the raw numbers OR • We can fit a curve (in red) that is a good model

Let’s See What I Mean • If we shade all the scores less than 6, what percentage of scores do you think we shaded?

Let’s See What I Mean • 30.3% or 287 people out of 947 • That means the total area of the bars would be 100% or a proportion of 1! 30.3%

Let’s See What I Mean • If we want to talk about the red curve, we make the total area below the curve 1. 30.3%

Let’s See What I Mean • The area below the curve less than 6 is 0.293. • That is 29.3% of the area which is less than 6. 30.3%

Let’s See What I Mean • The curve is a pretty good model for the bars! 30.3% 29.3%

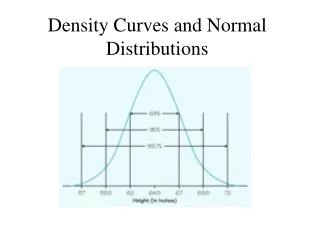
Density Curve • Is always on or above the horizontal axis • Has an area of 1 underneath it • A density curve describes the overall pattern of distribution. • The area under the curve and above any interval is the proportion of observations that fall in that interval.

Mean and Median Density Curves • Mean is the balancing point of the curve • Median is the marker of equal areas; divides the area under the curve in half.

Examples of Density Curves

Test • If the area to the left line in the density curve shown below is 0.40, what is the area of the other part? 0.40

Test • What percentage of observations are to the left of the line in the curve below? 0.40

Density Curves Are Sweet But… • There is one kind of curve that trumps them all. • We see it more than anything else • It is the basis of 95% of statistics.

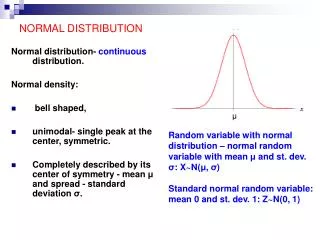
Normal Curves • Describe Normal Distributions • They are defined by two numbers • Mean: μ • Standard Deviation: σ (the average distance from the mean) • Bell Shaped

Normal Curves • They are defined by two numbers • Mean: μ • Standard Deviation: σ • Bell Shaped

Normal Curves • As usual, the area under the curve is 1 • Let’s take a look. • http://www-stat.stanford.edu/~naras/jsm/NormalDensity/NormalDensity.html

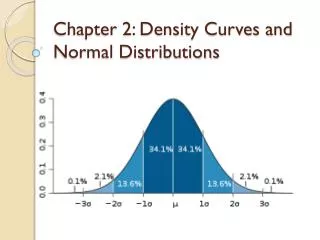
The 68-95-99.7 Rule • In the Normal distribution with mean μ and standard deviation σ: About 68% of observations fall within σ of μ. About 95% of observations fall within 2σof μ. About 99.7% of observations fall within 3σof μ.

The 68-95-99.7 Rule

Almost Done • Usually we define a Normal curve like this • N(μ, σ) • N(6, 1) means we have a curve with mean 6 and standard deviation 1. • Using our 68-95-99.7 Rule… 6-1=5 and 6+1=7 68% of the observations are between 5 and 7.

Practice • I make candies. The mean mass of the candy is 100g and the standard deviation is 5. • Draw a Normal curve for the situation. • What percentage of candies is between 95g and 105g? • What percentage of candies is less than 105g?

Practice • I make throw frisbees. My mean throw is 75 yards with a standard deviation of 5 yards • Draw a Normal curve for the situation. • What percentage of throws is between 65 and 85 yards? • What percentage of throws is less than above 70 yards?

Your Turn • Spend 15 minutes doing this worksheet. • You may work with those around you. • If you do not finish it is homework.

Standard Deviation Practice? • 1, 4, 5, 5, 6, 9 • Find the standard deviation

Density Curves and Normal Distribution