1 / 9

Understanding Sequential Circuit Analysis: States, Outputs, and Models

This document provides a comprehensive analysis of sequential circuits, focusing on the behavior of state, inputs, and outputs over time. It details how the current state at time (t) is stored in flip-flops and how the next state at time (t+1) and outputs depend on both current state and inputs. The differences between Mealy and Moore machines are explained, along with examples of state diagrams and state tables. Learn to derive output functions and next state functions, key features in designing and analyzing complex digital systems.

oona
Télécharger la présentation

Understanding Sequential Circuit Analysis: States, Outputs, and Models

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

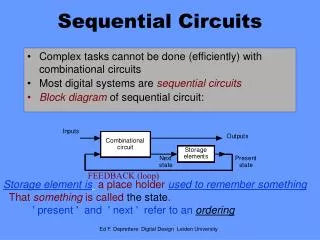
  1. SequentialCircuits Analysis

  2. Inputs Combina-tional Logic Outputs Storage Elements Next State State CLK Sequential Circuit Analysis • Current Stateat time (t) is stored in an array of flip-flops. • Next State at time (t+1) is a Boolean function of State and Inputs. • Outputsat time (t) are a Boolean function of State (t) and (sometimes) Inputs (t).

  3. Example of a SequentialCircuit Input: x(t) Output:y(t) State:(A(t), B(t)) • What is theOutput Function? • What is the Next State Function? x A Q D A Q C Next State B Q D CP Q' C y Output

  4. Present State Input Next State Output Present Next State Output A(t) B(t) x(t) A(t+1) B(t+1) y(t) State x(t)=0 x(t)=1 x(t)=0 x(t)=1 0 0 0 0 0 0 A(t) B(t) A(t+1)B(t+1) A(t+1)B(t+1) y(t) y(t) 0 0 1 0 1 0 0 1 0 0 0 1 0 0 0 0 0 1 0 0 0 1 1 1 1 0 0 1 0 0 1 1 1 0 1 0 0 0 0 1 1 0 0 0 1 0 1 0 1 0 1 1 0 0 1 1 0 0 1 0 1 0 1 1 0 0 0 1 1 1 1 1 0 0 State Table A(t+1) = A(t)x(t)+B(t)x(t) B(t+1) =A (t)x(t) y(t) =x (t)(B(t)+A(t))

  5. x=0/y=0 x=0/y=1 x=1/y=0 A B 1 0 0 0 x=0/y=1 x=1/y=0 x=1/y=0 x=0/y=1 1 1 0 1 x=1/y=0 State Diagrams • The sequential circuit function can be represented in graphical form as a state diagram

  6. MEALY MACHINE MOORE MACHINE Inputs X(t) Outputs Z(t) Inputs X(t) Combinational circuits Combinational circuits Storage Element S(t) Storage Element S(t) Outputs Z(t) Moore and Mealy Models • Moore Model • Outputs are a function ONLY of states • Mealy Model • Outputs are a function of inputs AND states

  7. x=1/y=0 x=0/y=0 1 0 Present Next State Output x=0/y=0 State x=0 x=1 x=0 x=1 x=1/y=1 0 0 1 0 0 x=0 1 0 1 0 1 0/0 x=0 Present Next State Output x=1 State x=0 x=1 x=1 x=0 0 0 1 0 1 0 2 0 2/1 1/0 2 0 2 1 x=1 Moore and Mealy Example StateDiagrams Mealy Moore

  8. 0/0 1/0 S0 S1 0/1 0 1 1/0 0/1 S0/0 S1 0/1 S2 0/1 1/0 1/0 0/1 0/0 1/0 1/0 S0 S1 S3 S2 0/1 1/0 1/0 Equivalent States • Twostatesareequivalentif: • Outputproducedforeachinput is identical • Thenextstatesforeachinputaresameorequivalent

  9. A Z D Q Q C R B D Q Q C R C D Q Clock Q C R Reset SequentialAnalysisExample • Variables • Inputs: None • Outputs: Z • State Variables: A, B, C • FlipFlopInputEquations • A(t+1) = • B(t+1) = • C(t+1) = • Z = Mealy? Moore? StateTable? StateDiagram?

More Related