Revisiting Hierarchical Quorum Systems

1. Henry Canivel Revisiting Hierarchical Quorum Systems Nuno Preguiça, J. Legatheaux Martins

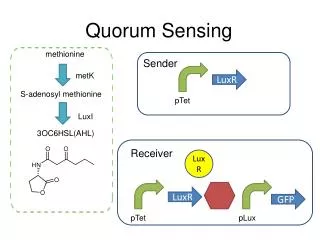
2. Purpose of Quorum Systems • Used as coordination tool • Data Replication Protocols • Location Management Algorithms • Masking Byzantine Failures

3. Quorum System Characteristics • Quorum size: number of nodes that need to be contacted to form a quorum • Basic: smallest majority vote • Advanced: majority vote dependent on structure • Grid: 2 n - 1 (size = n nodes or processes) • Unstructured: n/2 + 1 (size = n)

4. Quorum System Characteristics • Failure probability: chance that all quorums are unavailable (I.e. the system is unusable) • General: p < 0.5 • Load of a system: frequency of access of each element in the system

5. Quorum System Topologies • Triangle • Diamond • Grid • Hierarchical

6. Preliminary Information • Simplistic probabilistic failure model • Only crash failures • Only in transient

7. Failure probability • p <= 0.5 • If p > 0.5, then impossible to improve the availability when introducing new elements into quorum system

8. Grid Quorums

9. Operational Quorums • Read • Write • Read-Write

10. Read Quorum • Formed by obtaining a row-cover in the logical object on top of hierarchy • an object in level i is formed by obtaining a row-cover in at least 1 object of every row of the level i-1 grid

11. Write Quorum • Formed by obtaining a full-line in the logical object on top of hierarchy • Full-line in an object in level i is formed by obtaining a full-line in at least 1 object of every row of the level i-1 grid

12. Read-Write Quorum • Combination of both read and write • Full-line and row-cover • Note: creates conflict when mutual exclusion is only operation necessary

13. Hierarchical Quorum System • Quorum created recursively from root • Obtain quorum in majority of subtrees • Changes: • Quorum size smaller than average • Improve availability • Reduce load size for system

14. Hierarchical T-grid Algorithm • Obtaining Grid Quorum • Obtain quorum in majority of subtrees • Changes: • Quorum size smaller than average • Improve availability • Reduce load size for system

15. Hierarchical T-grid Algorithm • Obtaining Grid Quorum • Intersection of full-line and partial row cover • Partial row-cover vs. Full row cover • Full: level i object and at least 1 of every row in level i-1 • Partial: sans level i

16. Hierarchical T-grid Algorithm • h-T-grid algorithm still intersects with full cover • Improves failure probability by approximately 7.5-10% • h-T-grid algorithm holds greater improvements for rectangular grids • Failure probability = 1/3 of h-grid • # lines > # columns • Variable load and quorum size

17. Hierarchical T-grid • Two sub-triangles and a sub-grid • Recursive

18. Hierarchical T-grid Quorum • If triangle has a single line, quorum composed by element in the line • If more than one line, quorum can be obtained one of three methods: • If A is a quorum in T1 and B is quorum in T2, A U B in triangle of level m • If A is a quorum in T1 and B is a row cover in G, A U B is a quorum in triangle of level m • If A is a quorum in T2, B is a full-line in G, A U B is a quorum in triangle in level m

19. Hierarchical Triangle

20. Hierarchical Triangle • Minimizes load • Easier to introduce new nodes (expand system) • All quorums have the same size • Minimize volume of messages passed on scaling system

21. Final Notes • Larger quorums -> larger loads • Majority and HQS at top • h-T-grid • h-triang at bottom

22. Final Notes • Modifications to HQS • Reduce quorum size • Improve availability and load • Maintains stability at the least for slightly rectangular grids • Introduction to triangular QS • Better availability and load than grid-based • Quorum size always constant and smaller than avg quorum size in grid • Load almost optimal when analyzed from high availability

23. Comprenez-vous?