P( x , y )
440 likes | 748 Vues
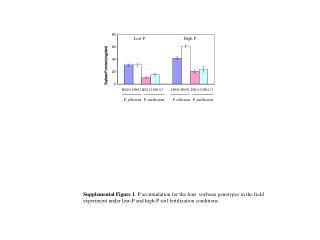
一、圓的標準式. 1. 圓的意義: 平面上與定點 ( 圓心 ) 的距離是定值 ( 半徑 ) 的. 所有點所成的圖形稱為 圓 。. 2. 圓的標準式: 以 Q( h k ) 為圓心, r 為半徑的圓方程式為. ( x h ) 2 + ( y k ) 2 = r 2 。. y. 證明: 若 P ( x y ) 是圓 C 上任意一點,. P( x , y ). r. r. r. r. r. r. r. r. Q( h , k ). r. r. 因此圓上的點 P ( x y ) 都滿足方程式. r. r.

P( x , y )
E N D
Presentation Transcript
一、圓的標準式 1. 圓的意義:平面上與定點(圓心)的距離是定值(半徑)的 所有點所成的圖形稱為圓。 2. 圓的標準式:以 Q(h k)為圓心,r為半徑的圓方程式為 (xh)2 + (yk)2 = r2。 y 證明:若 P(x y)是圓 C上任意一點, P(x, y) r r r r r r r r Q(h, k) r r 因此圓上的點 P(x y)都滿足方程式 r r (xh)2 + (yk)2 = r2。 x O 反之,若點 A(x1 y1)滿足方程式 (xh)2 + (yk)2 = r2。 = r。 即所有滿足方程式的點 A到 Q的距離都等於r。 因此, (xh)2 + (yk)2 = r2即為圓 C的方程式。 本段結束 稱之為圓 C的標準式。
3. 範例:(1) 求圓心為點 (2, 3),半徑為 4 的圓方程式。 (2) 設圓 C:(x3)2 + (y+1)2 = 1,求與圓 C 有相同的圓心 且面積為圓 C 面積 2 倍的圓方程式。 (x 2)2 + [y (3)]2 = 42 解:(1) 圓心 (2 3),半徑 4 (x2)2 + (y+3)2 = 16。 (2) 圓 C:(x3)2 + (y+1)2 = 1的圓心為 (3 1),半徑為 1, 圓面積為 2倍 故所求圓方程式為 (x3)2 + (y+1)2 = 2。 Let’s do an exercise !
馬上練習:(1) 求圓心為點 (0, 0),半徑為 1 的圓方程式。 (2) 與圓 C:(x3)2 + y2 = 16 有相同的圓心, 且圓周長為圓 C 一半的圓方程式。 解:(1) 圓心 (0 0),半徑 1 (x0)2 + (y0)2 = 12 x2 + y2 = 1。 (2) 圓 C:(x3)2 + y2 = 42的圓心為 (3 0),半徑為 4, 半徑為一半 圓周長為一半 所求圓半徑為 2。 故所求圓方程式為 (x3)2 + y2 = 4。 #
4. 範例:設 A(4, 9),B(6, 3), 解: B(6, 3) A(4, 9) Q 故所求圓方程式為 (x5)2 + (y6)2 =10。 Let’s do an exercise ! 馬上練習:設 A(2, 3),B(6, 1), 解: B(6, 1) A(2, 3) Q 故所求圓方程式為 (x4)2 + (y1)2 = 8。 #
5. 點與圓的關係:設點 P(x0 , y0)與圓 C: (xh)2 + (yk)2 = r2, 令圓心為 Q,半徑為r, P (1) 點 P在圓 C內部 P r P (2) 點 P在圓 C上 Q(h, k) (3) 點P在圓 C外部 範例:求以點 Q(2, 3) 為圓心,通過點 P(5, 1) 的圓方程式,並判斷 A(6 0),B(2 1),C(0 2) 是在圓內、圓外還是圓上。 解: 圓:(x2)2 + (y+3)2 = 25。 = 5 點 A在圓上。 點 B在圓內。 < 5 > 5 點 C在圓外。 Let’s do an exercise !
馬上練習:設圓 C:x2 + y2 = k, (2) 若 P(1 2) 在圓 C 內部,Q(3 3)在圓 C 外部, 求 k 的範圍。 解: (2) P(1 2)在圓內部 12 + (2)2 < k k> 5。 Q(3 3 )在圓外部 (3)2 + 32 > k k< 18。 故 5 < k< 18。 #
6. 範例:自 P(1, 2) 作圓 x2 + y2 4x + 2y 4 = 0 的兩條切線, 得切點 A、B,求 PAB 的外接圓方程式。 令 Q(2 1) 解:x2 + y2 4x + 2y 4 = 0 (x2)2 + (y+1)2 = 9, 因為 PAQ + PBQ = 180 PAQB四點共圓。 A Q P B 即 x2 + y2 3x y = 0。 Let’s do an exercise ! 注意:若四邊形的對角互補 圓內接四邊形(四點共圓)
馬上練習:自原點 O 作圓 x2 + y2 + 2x 4y + 1 = 0 的兩條切線, 得切點 P、Q,求 OPQ 的外接圓方程式。 解:x2 + y2 + 2x 4y + 1 = 0 (x+1)2 + (y2)2 = 4, 令 C(1 2) 因為 OPC + OQC = 180 OPCQ四點共圓。 P C O Q 即 x2 + y2 + x 2y = 0。 #
7. 範例:求過 A(1, 1),B(2, 2),且與 x 軸相切的圓方程式。 = 1 解: L r B(2,2) Q 設圓心 Q(x, y) x + y = 3, r A(1,1) x 故所求為 (x2)2 + (y1)2 = 1或 (x+2)2 + (y5)2 = 25。 注意:圓心到切線的垂直距離等於圓的半徑 r。 Let’s do an exercise !
馬上練習:設一圓通過 A(1, 2),B(3, 4),且圓心 在直線 L:2x y + 4 = 0上,求此圓的方程式。 = 3 解: M B r Q r A L #
8. 地震波:地震發生時會產生兩種波: (1) 縱波(又稱 P 波):振動方向與傳播方向一致,傳播速度快。 (2) 橫波(又稱 S 波):振動方向與傳播方向垂直,傳播速度慢。 由於縱波速度比橫波快,因此地震時先感覺到上下振動, 再感覺到左右搖晃。 觀測站所接收到的第一個訊號為縱波,而後才是橫波, 利用兩者的時間差,可估算出觀測站與震央的距離。 To be continued 範 例
範例:設某地震發生時,甲、乙、丙三個測站測得 P 波與 S 波 的時間差分別為 5 秒、10 秒、13 秒, 若此地區的 P 波速率為 6 (公里/秒),S 波速率為 4 (公里/秒), (1) 求震央到甲、乙、丙三個測站的距離。 (2) 若坐標平面的 1 單位長為 12 公里,且甲、乙、丙三個測站 在坐標平面上的位置分別為 O(0, 0),A(3, 12), B(8, 16), 求震央在坐標平面上的位置。 解: To be continued (2)
(2) 若坐標平面的 1 單位長為 12 公里,且甲、乙、丙三個測站 在坐標平面上的位置分別為 O(0, 0),A(3, 12), B(8, 16), 求震央在坐標平面上的位置。 解: (2) B(8,16) A(3,12) (3, 4) O(0,0) 故所求為 (3, 4)。 #
二、圓的一般式 1. 圓的一般式:將圓的標準式 (xh)2 + (yk)2 = r2 展開得 x2 + y2 2hx 2ky + h2 + k2 r2 = 0, 這是形如 x2 + y2 + dx + ey + f = 0 的方程式,稱之為圓的一般式。 反之,圓的一般式,分別對 x,y配方,也可化成標準式。 配方 即 x2+y2+dx+ey+f=0 (一般式) (xh)2+(yk)2 = (標準式)。 展開 (1) 若 > 0, 則圖形為一圓,圓心為 (h k), (2) 若 = 0, 則圖形為一點,即點 (h k)。 (3) 若 < 0, 則圖形中沒有點,即圖形不存在。 本段結束
2. 範例:說明下列方程式所代表的圖形。 (1) x2 + y2 2x + 6y + 6 = 0 (2) x2 + y2 2x + 6y + 10 = 0 (3) x2 + y2 2x + 6y + 16 = 0。 解:(1) 利用配方法,得 (x22x+1) + (y2+6y+9) = 6 + 1 + 9, (x1)2 + (y+3)2 = 4, 其圖形為圓心 (1 3),半徑為 2的圓。 (2) 利用配方法,得 (x22x+1) + (y2+6y+9) = 10 + 1 + 9, (x1)2 + (y+3)2 = 0, 可得 (x y) = (1 3),其圖形為一點(1 3)。 (3) 利用配方法,得 (x22x+1) + (y2+6y+9) = 16 + 1 + 9 , (x1)2 + (y+3)2 = 6, 此方程式沒有實數解,其圖形不存在。 Let’s do an exercise !
馬上練習:試判斷下列方程式所代表的圖形: (1) x2 + y2 4x + 6y 12 = 0 (2) x2 + y2 4x + 6y + 13 = 0 (3) x2 + y2 4x + 6y + 17 = 0。 解:(1) 利用配方法,得 (x24x+4) + (y2+6y+9) = 12 + 4 + 9, (x2)2 + (y+3)2 = 25, 其圖形為圓心 (2 3),半徑為 5的圓。 (2) 利用配方法,得 (x24x+4) + (y2+6y+9) = 13 + 4 + 9, (x2)2 + (y+3)2 = 0, 可得 (x y)=(2 3),其圖形為一點 (2 3)。 (3) 利用配方法,得 (x24x+4) + (y2+6y+9) = 17 + 4 + 9, (x2)2 + (y+3)2 = 4, # 此方程式沒有實數解,其圖形不存在。
3. 範例:求通過 A(1, 1),B(1, 1),C(2, 1) 三點的圓方程式。 解:設所求的圓方程式為 x2 + y2 + dx + ey + f = 0 則 解得 d = 1,e = 0,f = 3, 故所求為 x2 + y2 + x 3 = 0。 Let’s do an exercise !
馬上練習:設一圓通過 O(0 0),P(1 1),Q(4 2) 三點, 求其圓心與半徑。 解:設所求的圓方程式為 x2 + y2 + dx + ey + f = 0 解得 d = 8,e = 6,f = 0 x2 + y2 8x + 6y = 0, 其圓心 (4 , 3),半徑 5。 即 (x4)2 + (y+3)2 = 25, #
4. 範例:已知實數 x,y 滿足 x2 + y2 4x 2y + 4 = 0, 求 x2 (y1)2的最大值。 (x2)2 (y1)2 = 1 解:x2 + y2 4x 2y + 4 = 0 x2 (y1)2即為點(x y)與 A(0 1)兩點距離的平方。 由右圖可知圓上的點與 A(0 1)的最大距離 y = 3, 故所求最大值為 3 2 = 9。 A(0, 1) 3 Q(2, 1) Let’s do an exercise ! x O
馬上練習:已知實數 x,y 滿足 (x+2)2 (y1)2 = 9, 求 (x+5)2 (y5)2的最小值。 解:(x+2)2 (y1)2 = 32 (x+5)2 (y5)2即為點 (x y)與 A(5 5)兩點距離的平方。 由右圖可知圓上的點與 A(5 5)的最小距離 A(5 5) = 2, 2 Q(2, 1) 故所求最小值為 2 2 = 4。 #
5. 範例:A(0 0),B(30 0),若 P(x y) 為平面上動點, 求所有 P 點所成軌跡的方程式。 解: y P x A x2 + y2 = 4[ (x30)2 + y2 ] B (x 40)2 y2 = 400。 故所有 P點所成的圖形為一圓,圓心 (40 0),半徑為 20。 Let’s do an exercise !
馬上練習:已知 A(3 0),B(3 0),若 P(xy) 為平面上動點, 求所有 P 點所成軌跡的方程式。 y 解: P x A B (x+3)2 + y2 = 2[ (x3)2 + y2 ] (x 9)2 y2 = 72。 故所有 P點所成的圖形為一圓,圓心(9 0), # To be continued 注 意
注意:阿波羅尼斯圓: 設 A、B 為平面上兩相異點,P為動點, (1) 當 k = 1時, P 所有點 P的圖形為 B A (2) 當 k 1時,所有點 P的圖形為一圓。 例如: k = 2, k = 3, 的情形, 如右圖所示。 P P k=2 P k=3 本段結束 A B
6. 範例:設 A(4, 9),B(6, 3), 之 P 點的軌跡方程式。 P(x, y) A(4, 9) 解:設 P(xy), Q B(6, 3) 整理得 x2 + y2 10x 12y + 51 = 0。 故所求軌跡為一圓:x2 + y2 10x 12y + 51 = 0,其中 P A、B。 Let’s do an exercise !
馬上練習:設 A(2, 3),B(5, 1), 之 P 點的軌跡方程式。 A(2, 3) P(x, y) 解:設 P(xy), Q B(5, 1) 整理得 x2 + y2 7x 2y + 7 = 0。 故所求軌跡為一圓:x2 + y2 7x 2y + 7 = 0,其中 P A、B。 #
7. 範例:設點 A(2, 0),求圓 x2 + y2 = 9 中過點 A 的 所有弦中點的軌跡方程式。 解:設 P(x y)為過點 A的弦之中點, P O A 整理得x2 + y2 2x = 0。 故所求的軌跡圖形為一圓:x2 + y2 2x = 0。 Let’s do an exercise !
馬上練習:已知 A(0, 1) 為圓 (x2)2 + (y1)2 = 16 內部一點, 求過 A 點的所有弦中點的軌跡方程式。 解:設 P(x y)為過點 A的弦之中點, Q P A 整理得x2 + y2 2x 1 = 0。 故所求的軌跡圖形為一圓:x2 + y2 2x 1 = 0。 #
三、直線與圓的關係 1. 直線與圓:設一直線 L:ax+by+c=0 與圓 C:x2+y2+dx+ey+f=0, 令圓心 Q, (1) d(Q, L) <r L與圓 C 交於兩點(相割) 方程組有兩相異實數解。 (2) d(Q, L) =r L與圓 C 交於一點(相切) 方程組恰有一實數解。 (3) d(Q, L) >r L與圓 C 不相交(相離) 方程組沒有實數解。 Q Q Q L L L d(Q, L) < r d(Q, L) = r d(Q, L) > r 本段結束
2. 範例:求直線 L:x y + 1 = 0 與圓 C:x2+ y2 = 5 的交點。 y 解:將 L:y = x + 1代入x2+ y2 = 5, L:xy+1=0 (1, 2) 得 x2+ (x+1)2 = 5, x 解得 x = 1或 2。 O (2, 1) 即直線 L與圓 C和相交 於 (1 2)和 (2 1)兩點。 Let’s do an exercise !
馬上練習:求直線 L:x + y 3 = 0 與圓 C:(x+1)2 + y2 = 8 的交點。 解:將 L:y = 3 x代入 (x+1)2+ y2 = 8, x+y3=0 得 (x+1)2+ (3x)2 = 8, (1, 2) 解得 x = 1。 Q(10) 即直線 L與圓 C和相切於點 (1 2)。 #
3. 範例:若 P(3, 5) 為圓 C:x2 + y2 2x + 4y 11 = 0 的弦中點, 求此弦長及弦所在直線方程式。 (x1)2 + (y+2)2 = 16, 解:由 x2 + y2 2x + 4y 11 = 0 得圓心 Q(1, 2),半徑 r = 4, Q L 4 P 因弦心距必垂直平分弦, 且過 P(3, 5), 故所求為 2x 3y 21 = 0。 Let’s do an exercise !
馬上練習:若 P(1, 2) 為圓 C:x2 + y2 2x 2y 7 = 0 的弦中點, 求此弦長及弦所在直線方程式。 (x1)2 + (y1)2 = 9, 解:由 x2 + y2 2x 2y 7 = 0 得圓心 Q(1, 1),半徑r = 3, Q L 3 P = 4。 得所求直線斜率為 2, 因弦心距必垂直平分弦, 故所求為 2x y + 4 = 0。 且過 P(1, 2), #
4. 範例:試就實數 m 的範圍,討論直線 L:y = mx + 2 與圓 C:x2+ y2 = 1 的相交情形。 解: y A(0 2) (1) 判別式> 0 x 此時圓 C和直線 L相交於兩點。 O (2) 判別式= 0 此時圓 C和直線 L相切於一點。 Let’s do an exercise ! (3) 判別式< 0 此時圓 C和直線 L不相交。 直線 L 恆過點 A(0 2)。 注意:直線 L:y=mx+2 的點斜式為 y2=m(x0)
馬上練習:試就實數 k 的範圍,討論直線 L:y = x k 與圓 C:x2+ y2 = 2 的相交情形。 解: y y=x+2 (1) 判別式> 0 y=x2 x 此時圓 C和直線 L相交於兩點。 O (2) 判別式= 0 此時圓 C和直線 L相切於一點。 (3) 判別式< 0 此時圓 C和直線 L不相交。 #
5. 「圓上」已知點的切線方程式: (圓心到切點的斜率)(切線的斜率) = 1 。 範例:求通過圓 (x1)2 + (y+2)2= 25 上一點 A(4 2) 的切線方程式 解:令圓心 Q(1 2) 3x + 4y = 20 A(4, 2) Q(12) 設切線:3x + 4y = k。 又切線過 A(4 2 ) k = 34+ 42 = 20。 故所求切線為 3x + 4y = 20。 Let’s do an exercise !
馬上練習:求通過 A(1 4) 且與圓 (x2)2 + (y+1)2 = 26 相切的直線方程式。 解:令圓心 Q(2 1) Q(21) = 5 。 A(1, 4) 設切線:x 5y = k。 x 5y + 19 = 0 又切線過 A(1 4 ) = 19。 k = 1 54 故所求切線為 x 5y + 19 = 0。 #
6. 範例:直線 L:8x 3y + a = 0 與圓 x2 + y2 + 2x y + b = 0, 相切於點 P(c 1),求 a、b、c 。 解: P (3, 1) 8x 3y 27 = 0 c = 3 切點 P(31)。 P(31)代入 L:8x 3y + a = 0, 得 a = 27。 P(31)代入 x2 + y2 + 2x y + b = 0, 得 b = 17。 故所求 a = 27 , b = 17 , c = 3。 #
7. 已知切線斜率為 m 的切線方程式: 設切線 y = mx + k, 利用相切 判別式 = 0。 範例:設圓 C:x2 + y2 2y 4 = 0,求斜率為 2 且與圓 C 相切的直線方程式。 y=2x+6 解:設切線 L:y = 2x + k, y=2x4 Q ∵相切 ∴ 判別式 = 0 故所求切線為 y = 2x + 6或 y = 2x 4。 Let’s do an exercise !
馬上練習:設圓 C:x2 + y2 = 5,求斜率為 2 且與圓 C 相切的直線方程式。 解:設切線 L:y = 2x + k, Q y=2x+5 ∵相切 ∴ 判別式 = 0 y=2x5 故所求切線為 y = 2x + 5或 y = 2x 5。 #
8. 「圓外」已知點 (x0 , y0) 的切線方程式: 設切線 y y0 = m(xx0), 利用相切 判別式 = 0。 範例:(1)求點 P(1 2) 到圓 C:(x4)2 + (y3)2 = 5 的切線段長。 (2)求過點 P(1 2)且圓 C:(x4)2 + (y3)2 =5 相切的直線方程式。 L 解: A P(1, 2) (2) 設切線斜率為 m 切線:y2=m(x1), Q(4, 3) L ∵相切∴判別式=0 因為切線必過點 (1 2), 故所求切線為 x + 2y = 5或 2x y = 0。 Let’s do an exercise !
馬上練習:(1) 求點 P(5 15) 到圓 C:x2 + y2 = 25 的切線段長。 (2) 求過點 P(5 15)且與圓 C:x2+y2=25 相切的直線方程式。 P(5,15) 解: 15 = 15。 (2) 設切線斜率為 m 切線:y 15 = m(x5), A 5 O L L ∵相切 ∴ 判別式= 0 又切線必過 (5 15) 一條切線 L的方程式:4x 3y + 25 = 0。 因為 P在圓外,必有兩條切線, 所以另一條切線為過 P(5 15)而無斜率的鉛垂線, 即 x = 5。 # 故所求為 4x 3y + 25 = 0與 x = 5。 注意:當點在圓外且切線斜率只能求出一解時,則另一條切線無斜率(即鉛垂線)。
9. 範例:在坐標平面上 (7 5) 處有一光源, 求將圓 x2 + (y1)2 = 1 投影到 x軸的影長。 P(7,5) 解:設切線斜率為 m 切線:y 5 = m(x7), L L Q(01) ∵ 相切 ∴ 判別式 = 0 A B y= 0 (x軸) 因為切線必過點 (7 5),即切線為 5x 12y = 25與 3x 4y = 1, 本 節 結 束
馬上練習:設 m 為實數, y = m(x+3) 在坐標平面上的兩個交點位於不同的象限,而滿足此 條件的 m 之最大範圍為 a < m < b,則 a = ? b = ? (化成最簡分數) <102數甲> 解: 此圓在 x軸上方, 若兩交點位於不同象限, 則必在一、二象限, y 設兩交點為 (x1y1) 、 (x2 y2) y=m(x+3) (x2y2) (x1y1) (2 1) x # O (3 0) To be continued 注 意
注意:若圓與直線 y = m(x+3)兩交點位於不同象限, y 由圖可知: y = m(x+3) (0 5) Q (0 2) (3 0) x O 本 節 結 束