1 / 32

Adding Error Bars to Column and Bar Graphs in Excel

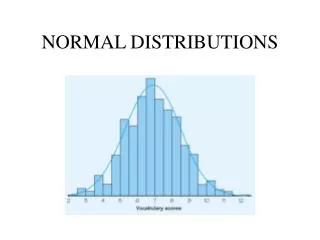
This guide explores the fundamental concepts of error bars in normal distributions, specifically how to add them to column and bar graphs in Excel. We cover the standard deviation as a measure of variability and demonstrate how to compute it alongside variance. Learn step-by-step methods to insert error bars, including selecting data points, formatting, and understanding systematic errors in your graphs. Enhance your data visualization skills while ensuring your representations accurately reflect variability in your datasets.

laasya
Télécharger la présentation

Adding Error Bars to Column and Bar Graphs in Excel

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

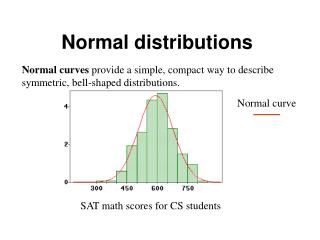
  1. Error Bars in Normal Distributions

  2. Error Bars in Column / Bar Graphs http://chandoo.org/wp/2010/07/12/gantt-box-chart-tutorial-template/ http://support2.dundas.com/OnlineDocumentation/winchart2005/ErrorBarsChart.html

  3. Standard Deviation, s Standard Deviation: A statistical measure of spread or variability. Computed as the root mean square (RMS) deviation of the values from their arithmetic mean. Variance: The square of the standard deviation. STDEV, sample of a larger population STDEVP, entire population

  4. Average & Error Barsin Column Graphs

  5. Compute Sigma

  6. Compute Sigma

  7. How to Add Error Bars

  8. How to Add Error Bars 3 2 1 5 4

  9. How to Add Error Bars Select the cell that contains the sigma value Type sigma here

  10. Average & Error Barsin Bar Graphs

  11. Average & Error Barsin Bar Graphs

  12. Average & Error Barsin Bar Graphs

  13. (X,Y) Scatter Graphs & Regression Bad example Better example

  14. How to Present (X,Y) Scatter Graphs, Compute Trendlines, and Extract Chemical Information using Excel Example: Chemical Kinetics & Equilibria SP10 Assign. #4 on Aspirin: Handout & online. SP11 Assign. #4 on pH-Indicator: Handout & online.

  15. AP11 Assignment #4

  16. AP11 Assignment #4

  17. AP11 Assignment #4 Your simulated spectrum will be the sum of the Gaussian functions that describe the absorbances of the three species: -- protonated dye -- neutral dye, and -- deprotonated dye.

  18. AP11 Assignment #4

  19. (X,Y) Built-In Functions

  20. (X,Y) Data Quadratic Function

  21. (X,Y) Data Quadratic Function

  22. (X,Y) Data Quadratic Function

  23. (X,Y) Data Quadratic Function

  24. (X,Y) Data Quadratic Function

  25. (X,Y) Data Quadratic Function

  26. (X,Y) Data Quadratic Function

  27. (X,Y) Data Quadratic Function

  28. (X,Y) Data QF: Y-Axis Error Bars 1. Left click the graph line to which you want to add error bars. 2-Mac: Control-click the selected line. 2-PC: Left-click the selected line. 3. Select “Format Data Series”.

  29. (X,Y) Data QF: Y-Axis Error Bars 3 1 2 4 5

  30. (X,Y) Data QF: Y-Axis Error Bars

  31. (X,Y) Data QF: Y-Axis Error Bars

  32. (X,Y) Data QF: Types of Errors Systematic error: All numbers in the sample will be too high! The precise function was y = x2 The sample data were computed with: y = [x+0.3*RAND()]2 The x-values were assumed to be error-free The fitted function was: y = 0.9937x2+ 0.3459x The STDEV of the y-values is 0.62 Systematic error: There should not be a linear term. This is were you notice the systematic error made (on purpose) in the sample data generation!

More Related