1 / 29

Junction tree Algorithm

Junction tree Algorithm. 10-708:Probabilistic Graphical Models Recitation: 10/04/07 Ramesh Nallapati. Cluster Graphs. A cluster graph K for a set of factors F is an undirected graph with the following properties: Each node i is associated with a subset C i ½ X

tomasso
Télécharger la présentation

Junction tree Algorithm

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

  1. Junction tree Algorithm 10-708:Probabilistic Graphical Models Recitation: 10/04/07 Ramesh Nallapati

  2. Cluster Graphs • A cluster graphK for a set of factors F is an undirected graph with the following properties: • Each node i is associated with a subset Ci½X • Family preserving property: each factor  is such that scope[] µ Ci • Each edge between Ci and Cj is associated with a sepset Sij = CiÅ Cj • Execution of variable elimination defines a cluster-graph • Each factor used in elimination becomes a cluster-node • An edge is drawn between two clusters if a message is passed between them in elimination • Example: Next slide 

  3. Variable Elimination to Junction Trees: • Original graph Coherence Difficulty Intelligence Grade SAT Letter Job Happy

  4. Variable Elimination to Junction Trees: • Moralized graph Coherence Difficulty Intelligence Grade SAT Letter Job Happy

  5. Variable Elimination to Junction Trees: • Triangulated graph Coherence Difficulty Intelligence Grade SAT Letter Job Happy

  6. Variable Elimination to Junction Trees: • Elimination ordering: C, D, I, H, G, S, L Coherence C,D D Difficulty Intelligence Grade SAT Letter Job Happy

  7. Variable Elimination to Junction Trees: • Elimination ordering: C, D, I, H, G, S, L Coherence C,D D Difficulty Intelligence D,I,G G,I Grade SAT Letter Job Happy

  8. Variable Elimination to Junction Trees: • Elimination ordering: C, D, I, H, G, S, L Coherence C,D D Difficulty Intelligence D,I,G G,I Grade SAT G,I,S Letter G,S Job Happy

  9. Variable Elimination to Junction Trees: • Elimination ordering: C, D, I, H, G, S, L Coherence C,D D Difficulty Intelligence D,I,G G,I Grade SAT G,I,S Letter G,S Job G,J Happy H,G,J

  10. Variable Elimination to Junction Trees: • Elimination ordering: C, D, I, H, G, S, L Coherence C,D D Difficulty Intelligence D,I,G G,I Grade SAT G,I,S Letter G,S J,S,L G,J,S,L Job G,J Happy H,G,J

  11. Variable Elimination to Junction Trees: • Elimination ordering: C, D, I, H, G, S, L Coherence C,D D Difficulty Intelligence D,I,G G,I Grade SAT G,I,S L,J Letter G,S J,S,L G,J,S,L J,S,L Job G,J Happy H,G,J

  12. Variable Elimination to Junction Trees: • Elimination ordering: C, D, I, H, G, S, L Coherence C,D D Difficulty Intelligence D,I,G G,I Grade L,J SAT G,I,S L,J Letter G,S J,S,L G,J,S,L J,S,L Job G,J Happy H,G,J

  13. Properties of Junction Tree C,D • Cluster-graph G induced by variable elimination is necessarily a tree • Reason: each intermediate factor is used atmost once • G satisfies Running Intersection Property (RIP) • (X 2 Ci & X in Cj) ) X 2 CK where Ck is in the path of Ci and Cj • If Ci and Cj are neighboring clusters, and Ci passes message mij to Cj, then scope[mij] = Si,j • Let F be set of factors over X. A cluster tree over F that satisfies RIP is called a junction tree • One can obtain a minimal junction tree by eliminating the sub-cliques • No redundancies D D,I,G G,I L,J G,I,S L,J G,S J,S,L G,J,S,L J,S,L G,J H,G,J

  14. Junction Trees to Variable elimination: • Now we will assume a junction tree and show how to do variable elimination 1: C,D Coherence D 2: G,I,D Difficulty Intelligence G,I 3: G,S,I Grade SAT G,S Letter 4: G,J,S,L Job G,J Happy 5: H,G,J

  15. Junction Trees to Variable Elimination: • Initialize potentials first: 01(C,D) = P(C)P(D|C) 1: C,D Coherence D 02(G,I,D) = P(G|D,I) 2: G,I,D Difficulty Intelligence G,I 03(G,S,I) = P(I)P(S|I) 3: G,S,I Grade SAT G,S 04(G,J,S,L) = P(L|G)P(J|S,L) Letter 4:G,J,S,L Job G,J 05(H,G,J) = P(H|G,J) Happy 5:H,G,J

  16. Junction Trees to Variable Elimination: • Pass messages: (C4 is the root) 01(C,D) = P(C)P(D|C) 1: C,D 1! 2(D) = C01(C,D) D 02(G,I,D) = P(G|D,I) 2: G,I,D 2! 3(G,I) = D02(G,I,D)1! 2(D) G,I 03(G,S,I) = P(I)P(S|I) 3: G,S,I 3! 4(G,S) = I03(G,S,I)2! 3(G,I) G,S 04(G,J,S,L) = P(L|G)P(J|S,L) 4:G,J,S,L 4(G,J,S,L) = 3 ! 4(G,S) 5 ! 4(G,J)04(G,J,S,L) G,J 05(H,G,J) = P(H|G,J) 5! 4(G,J) = H05(H,G,J) 5:H,G,J

  17. Junction Tree calibration • Aim is to compute marginals of each node using least computation • Similar to the 2-pass sum-product algorithm • Ci transmits a message to its neighbor Cj after it receives messages from all other neighbors • Called “Shafer-Shenoy” clique tree algorithm 3: G,S,I 1: C,D 2: G,I,D 4:G,J,S,L 5:H,G,J

  18. Message passing with division • Consider calibrated potential at node Ci whose neighbor is Cj • Consider message from Ci to Cj • Hence, one can write: Ci Cj

  19. Message passing with division • Belief-update or Lauritzen-Speigelhalter algorithm • Each cluster Ci maintains its fully updated current beliefs i • Each sepset sij maintains ij, the previous message passed between Ci-Cj regardless of direction • Any new message passed along Ci-Cj is divided by ij

  20. Belief Update message passingExample B 2: B,C C 3: C,D 1: A,B 23 = 3 ! 2(C) 12 = 1 ! 2(B) 2! 1(B) Actual message This is what we expect to send in the regular message passing!

  21. Belief Update message passingAnotherExample B 2: B,C C 3: C,D 1: A,B 2 ! 3(C) = 023 3 ! 2(C) = 123 This is exactly the message C2 would have received from C3 if C2 didn’t send an uninformed message: Order of messages doesn’t matter!

  22. Belief Update message passingJunction tree invariance • Recall: Junction Tree measure: • A message from Ci to Cj changes only j and ij: • Thus the measure remains unchanged for updated potentials too!

  23. Junction trees from Chordal graphs • Recall: A junction tree can be obtained by the induced graph from variable elimination • Alternative approach: using chordal graphs • Recall: • Any chordal graph has a clique tree • Can obtain chordal graphs through triangulation • Finding a minimum triangulation, where largest clique has minimum size is NP-hard

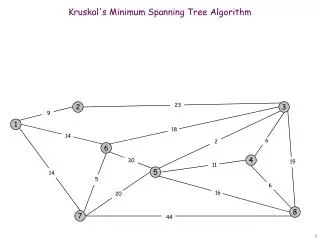
  24. Junction trees from Chordal graphsMaximum spanning tree algorithm • Original Graph Coherence Difficulty Intelligence Grade SAT Letter Job Happy

  25. Junction trees from Chordal graphsMaximum spanning tree algorithm • Undirected moralized graph Coherence Difficulty Intelligence Grade SAT Letter Job Happy

  26. Junction trees from Chordal graphsMaximum spanning tree algorithm • Chordal (Triangulated) graph Coherence Difficulty Intelligence Grade SAT Letter Job Happy

  27. Junction trees from Chordal graphsMaximum spanning tree algorithm • Cluster graph C,D Coherence 1 D,I,G 1 Difficulty Intelligence 2 1 1 G,I,S G,H Grade SAT 2 G,S,L 1 1 Letter 2 Job L,S,J Happy

  28. Junction trees from Chordal graphsMaximum spanning tree algorithm • Junction tree C,D Coherence D D,I,G Difficulty Intelligence G,I G G,I,S G,H Grade SAT G,S G,S,L Letter S,L Job L,S,J Happy

  29. Summary • Junction tree data-structure for exact inference on general graphs • Two methods • Shafer-Shenoy • Belief-update or Lauritzen-Speigelhalter • Constructing Junction tree from chordal graphs • Maximum spanning tree approach

More Related