1 / 8

Understanding Rotational Motion: Torque, Inertia, and Angular Momentum

Explore the fundamentals of rotational motion with a focus on Earth's rotation, torque, inertia, and angular momentum. Learn how the Earth revolves around the sun annually and rotates daily, affecting its rotational velocity. Discover how torque is calculated using force and lever-arm length, illustrated with a practical example involving a wrench. Understand the concept of balance on a seesaw through rotational inertia and how angular momentum plays a critical role in activities like bicycle riding. Engage with these principles and their real-world applications.

chester-ashley
Télécharger la présentation

Understanding Rotational Motion: Torque, Inertia, and Angular Momentum

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

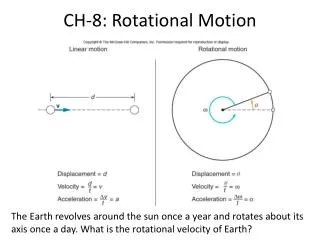
  1. CH-8: Rotational Motion The Earth revolves around the sun once a year and rotates about its axis once a day. What is the rotational velocity of Earth?

  2. Equations Sheet

  3. Torque, τ Torque depends on the applied force and lever-arm. Torque = Force x lever-arm Torque is a vector. It comes in clockwise and counter-clock wise directions. Unit of torque = N•m P: A force of 40 N is applied at the end of a wrench handle of length 20 cm in a direction perpendicular to the handle as shown above. What is the torque applied to the nut?

  4. Application of Torque: Weighing P. A child of mass 20 kg is located 2.5 m from the fulcrum or pivot point of a seesaw. Where must a child of mass 30 kg sit on the seesaw in order to provide balance?

  5. Rotational Inertia Rotational Inertia = mass x square of distance from axisI =mr2Rotational inertia is a scalar. Unit for I = kg.m2

  6. Expressions for Several objects

  7. Angular Momentum or Rotational Momentum Angular momentum is the product of the rotational inertia and rotational velocity. L = I·ω Conservation of Angular Momentum

  8. Angular momentum and Bicycles Explain the role of angular momentum in riding a bicycle?

More Related