1 / 18

Understanding Tangents and Secants: Circle Geometry Problems

This resource explores the relationship between line segments, tangents, and secants intersecting a circle. It provides practical problems involving the lengths of segments and the measures of angles formed by secants and tangents. Learn how to calculate missing lengths and angle measures with examples that cover different cases based on the vertex's location relative to the circle—inside, on, or outside. Ideal for students looking to deepen their understanding of circle geometry and related angle measures.

oleg-barnett
Télécharger la présentation

Understanding Tangents and Secants: Circle Geometry Problems

An Image/Link below is provided (as is) to download presentation Download Policy: Content on the Website is provided to you AS IS for your information and personal use and may not be sold / licensed / shared on other websites without getting consent from its author. Content is provided to you AS IS for your information and personal use only. Download presentation by click this link. While downloading, if for some reason you are not able to download a presentation, the publisher may have deleted the file from their server. During download, if you can't get a presentation, the file might be deleted by the publisher.

E N D

Presentation Transcript

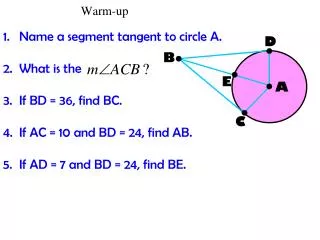
  1. Name a segment tangent to circle A. • What is the • If BD = 36, find BC. • If AC = 10 and BD = 24, find AB. • If AD = 7 and BD = 24, find BE. Warm-up D B E A C

  2. Unit Question:What happens when line segments intersect a circle? Today’s Question: How do you find the measure of angles formed by secant and tangent lines?

  3. Secant Anglesand Secant – Tangent Angles

  4. measure of an arc = measure of central angle m AB m ACB m AE A E 97 Q = 97° B C = 263° = 83°

  5. Case I:Vertex is ON the circle ANGLE ARC ARC ANGLE

  6. A secant line intersects the circle at exactly two points. SECANT sounds like second

  7. Ex. 1 Find m1. A B 1 124° C m<1 = 620

  8. Ex. 2 Find m1. 1 84° m<1 = 420

  9. Remember, a straight angle is 180 degrees!

  10. 108° Ex. 3 Find m1. 1 m<1 = 1260

  11. Case II:Vertex is inside the circle A ARC B ANGLE D ARC C Looks like a PLUS sign!

  12. Ex. 4 Find m1. 93° A B 1 D C 113° m<1 = 1030

  13. Ex. 5 Find mQT. mQT = 1000 N Q 840 920 M T

  14. Case III:Vertex is outside the circle C ANGLE small ARC A D LARGE ARC B LARGE ARC LARGE ARC small ARC ANGLE small ARC ANGLE

  15. Ex. 6 Find m1. 1 15° A D 65° B m<1 = 250

  16. Ex. 7 Find mAB. m AB = 160 A 27° 70° B

  17. Ex. 8 Find m1. 240° 1 m<1 = 600

  18. pg 214 #1-15

More Related