Motion Analysis using Optical flow
140 likes | 166 Vues
Understand the principles of optical flow for motion analysis, including deriving object properties and computing displacement vectors. Learn to apply optical flow in real-time motion detection and object tracking scenarios. Explore the computation rationale and methods involved in optical flow analysis.

Motion Analysis using Optical flow
E N D
Presentation Transcript
Motion Analysis using Optical flow CIS601 Longin Jan Latecki Fall 2003 CIS Dept of Temple University
Part 1: Motion Analysis • Usual input of a motion analysis system is a temporal image sequence • Motion analysis is often connected with real-time analysis
Three main groups of motion analysis problem • Motion detection: • - register any detected motion • - single static camera • Moving object detection and location: • -moving object detection only : motion based segmentation methods • - detection of a moving object, detection of the trajectory of its motion, prediction of its future trajectory: image object matching techniques are often used to solve these tasks (direct matching of image data, matching of object features, specific representative object points (corner etc.),represent moving object as graphs and matching these graphs); another useful method is optical flow • Derivation of 3D object properties:from a set of 2D projections of acquired at different time instants of object motion
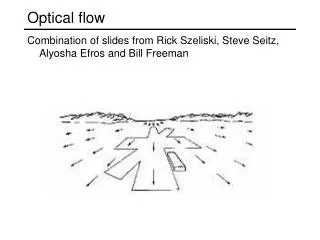
Optical flow • Reflects the image changes due to motion during a time interval dt, which is short enough to guarantee small inter-frame motion changes • The immediate objective of optical flow is to determine a velocity field:A 2D representation of a (generally) 3D motion is called a motion field (velocity field). Whereas each point is assigned a velocity vector corresponding the motion direction, velocity and distance from an observer at an appropriate image location • Based on 2 assumptions: - The observed brightness of any object point is constant over time - Nearby points in the image plane move in a similar manner(velocity smoothness constraint)
Optical flow Motion field is a projection of ‘real’ motion vectors of 3D objects to the image plane. We can only compute an optical flow from time-varying brightness in the image sequence, which is an approximation of the motion field.
Computation Rationale for Optical Flow • Let us suppose we have a continuous image, the image intensity is given by I(x,y,t), where the intensity is now a function of time t, as well as of x and y. • If this point (x,y) moves to a point (x+dx,y+dy) at time t+dt, the following equation holds, which we transform by Taylor expansion:
Thus, the displacement vector [dx/dt, dy/dt] at pixel (x,y) at frame t is the one for which the spatial derivative of the image intensity I at point (x,y) is equal to the minus of the temporal derivative of I at (x,y).
The aperture problem Only a component of the motion field in the direction of the spatial image gradient can be computed using this equation. This component is called the normal component, because the spatial image gradient is normal to the spatial direction along which the image intensity remains constant. See this link for a nice demo movie.
To compute the displacement vector [dx/dt, dy/dt] at pixel (x,y) at frame t we need at least two equations, but so far we have only one. We will consider two methods to obtain additional equations. The first method works for color videos, where we have red R, green G, and blue color intensity values: • Since this is an overdetermined system of equations, we have two ways to solve it: • Use least squares. • Disregard, say blue color, and use Gauss elimination. See an example Matlab program.
The second method ( from E. Trucco and A. Verri: Introductory Techniques for 3-D Computer Vision) Based on 2 assumptions: The observed brightness of any object point is constant over time Nearby points in the image plane move in a similar manner (velocity smoothness constraint) implies a constant motion vector field within a small patch of the image plane
Computation Method Homework (optional): Implement this algorithm and test on a synthetic and real image sequences.
Optical flow in motion analysis Motion, as it appears in dynamic images, is usually some combination of 4 basic elements: (a)Translation at constant distance from the observer. ---parallel motion vectors (b)Translation in depth relative to the observer. ---Vectors having common focus of expansion. (c) Rotation at constant distance from view axis. ---concentric motion vectors. (d) Rotation of planar object perpendicular to the view axis. ---- vectors starting from straight line segments.